中学受験の算数で出題される単元「和差算」。和と差の値がわかっていて、条件に適した数値を求める問題です。
和差算では、足し算、引き算、掛け算、割り算の4つの計算の考え方で答えを出すことができるのが特徴です。難しい計算は必要としませんが、考え方が少し難しい単元なので、戸惑ってしまう人も多いと思います。
しかし和差算は基本的な解き方さえおさえていれば、応用問題まで解くことができます。ですので基礎を徹底的に学習して得点源にしていきましょう。
今回は和差算について解説していきます。
- 算数が苦手な人
- 和差算を初めて学習する人
- 和差算が苦手な人
そのような人たちでも理解しやすいように、わかりやすく解説しています。
今回の記事を読むことで、和差算とは何か理解でき、線分図を使った解き方を習得できます。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
和差算① 和差算とは、和差算の公式
和差算とはいくつかの数量のうち、2つの数量の足し算の答え(和)と引き算の答え(差)に注目して、それぞれの数量を求める問題のことを言います。
二つの数字があれば、その二つの数字は大きい方の数字と小さい方の数字に分けられます。そしてその数字の和と差がわかっている場合、下の線分図のように表すことができます。
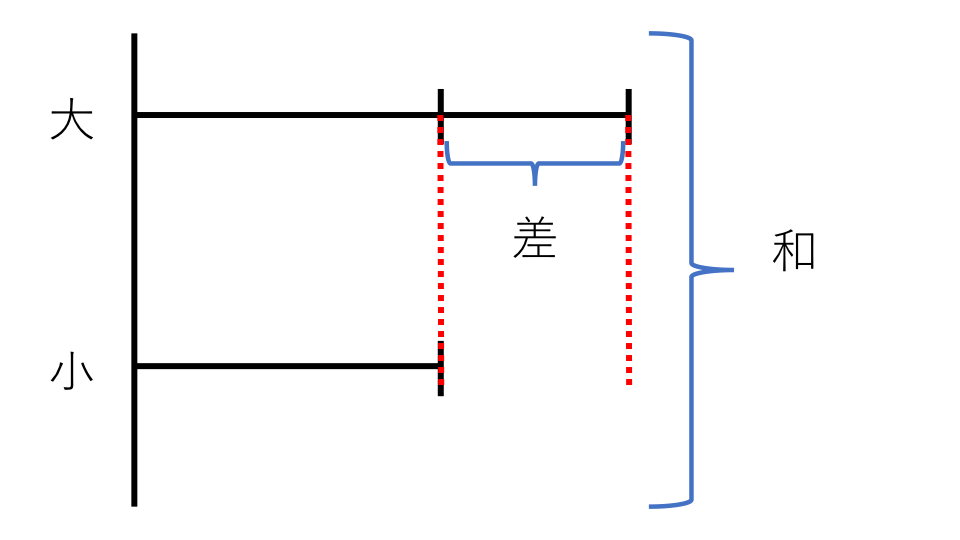
この線分図から公式を導き出すと
2つの数字の和と差がわかっている場合
- 大きい方の数字=(和+差)÷2
- 小さい方の数字=(和−差)÷2
線分図を書いて考えれば、導き出せる公式なので、この公式は覚えても覚えなくてもどちらでもいいです。しかし公式をただ意味も分からずに覚えるのはやめてください。
具体的な考え方は例題を使って説明していきます。
和差算② 基本問題
例題1
3年1組のクラスの人数は30人で男子は女子よりも8人多いそうです。3年1組のクラスの男子の人数と女子の人数はそれぞれ何人になるか求めなさい。
解説
男子と女子の人数の関係を線分図で表すと下の図のようになります。
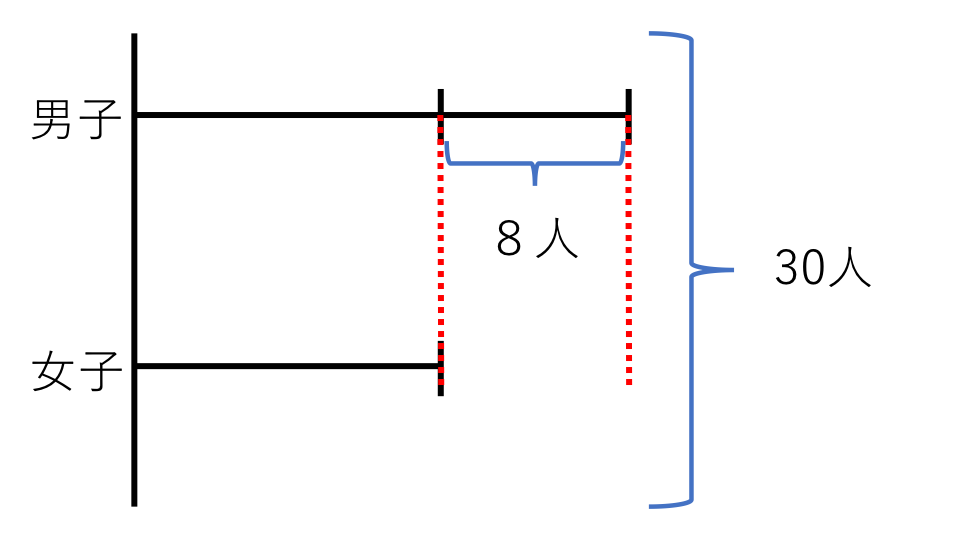
和の30人と差の8人を足すと、全体が男子の人数の2倍になるのがわかると思います。
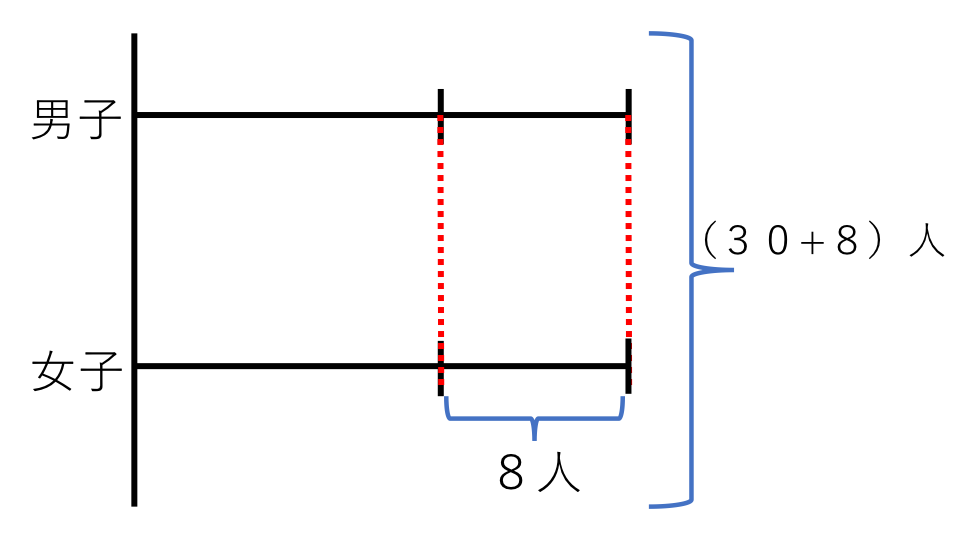
次に和の30人から差の8人をひくと全体が女子の人数の2倍になります。
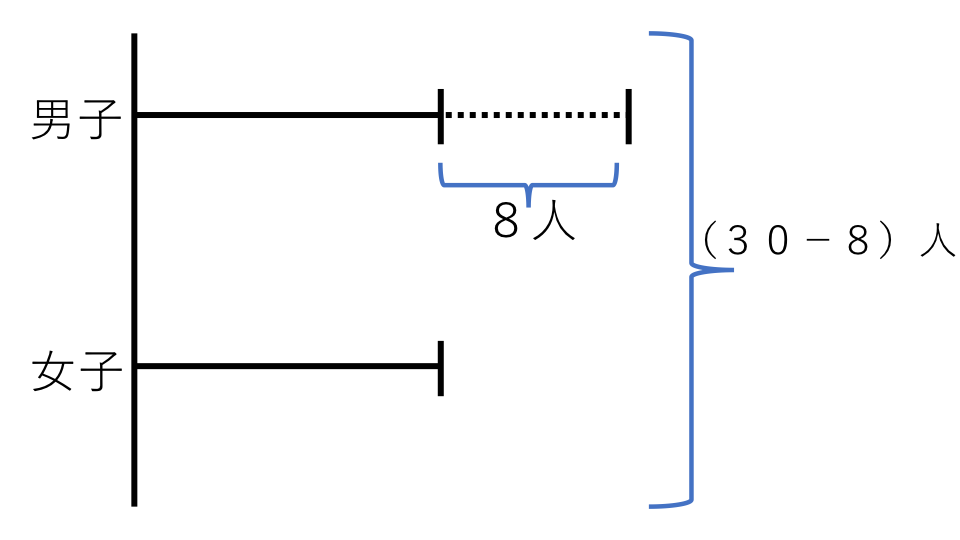
ですので男子の人数と女子の人数は、
男子の人数=(30+8)÷2=19人
女子の人数=(30-8)÷2=11人
よって答え男子19人、女子11人
一つひとつ丁寧に求めましたが、男子の人数がわかれば女子の人数もわかるので、全体から男子の人数を引いて女子の人数を求めても良いです。
例題2
AとBの2つの数字があります。AとBを足すと82、AからBを引くと34になります。このときのAとBの値を求めなさい。
解説
AとBの関係は足すと82になるので和は82、引くと34になるので差は34。この関係を線分図に表すと下の図のようになります。
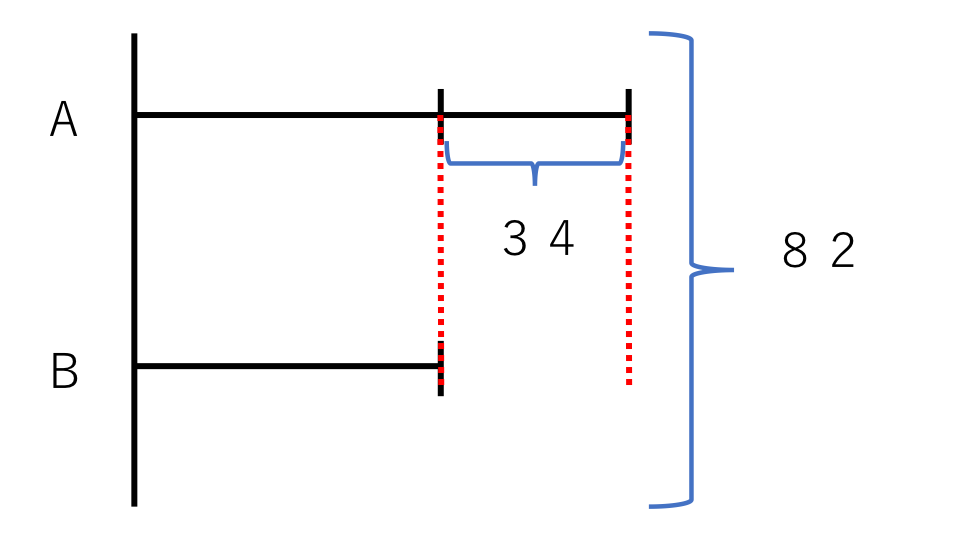
和の82に差の34を足すと、全体がAの数の2倍になります。
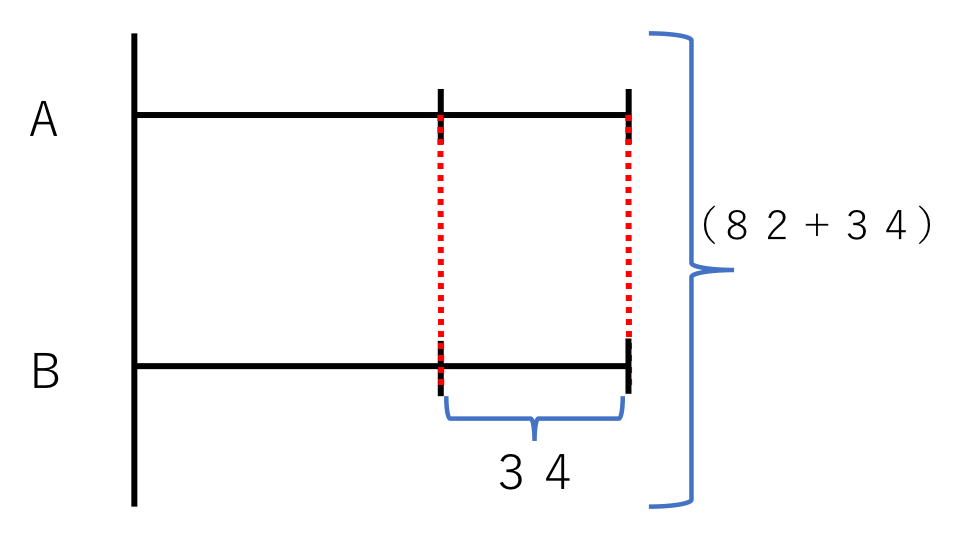
また82から差の34をひくと、全体がBの数の2倍になります。
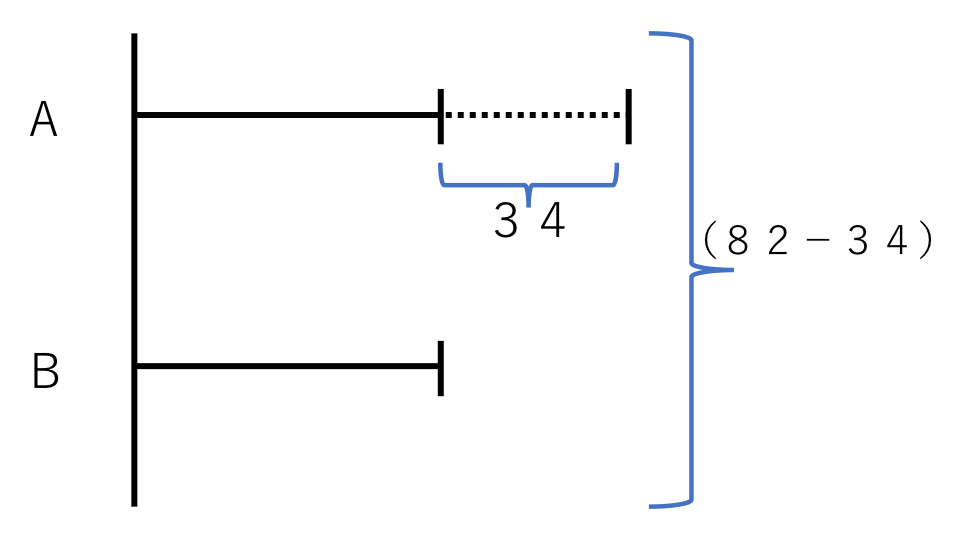
よって
A=(82+34)÷2=58
B=(82-34)÷2=24
よって答えA58、B24
例題3
ある日の昼の長さは、夜の長さよりも2時間長かったそうです。この日の昼の長さと夜の長さを求めなさい。
解説
問題文を見たときに和が示されていないからわからない、と思った人がいるのではないでしょうか。しかし1日は24時間と決まっているので和は24です。中学受験ではこのように一般常識を知っている前提の問題も出題されるので注意して問題文を読んでください。
昼と夜の関係を線分図に表すと下の図のようになります。
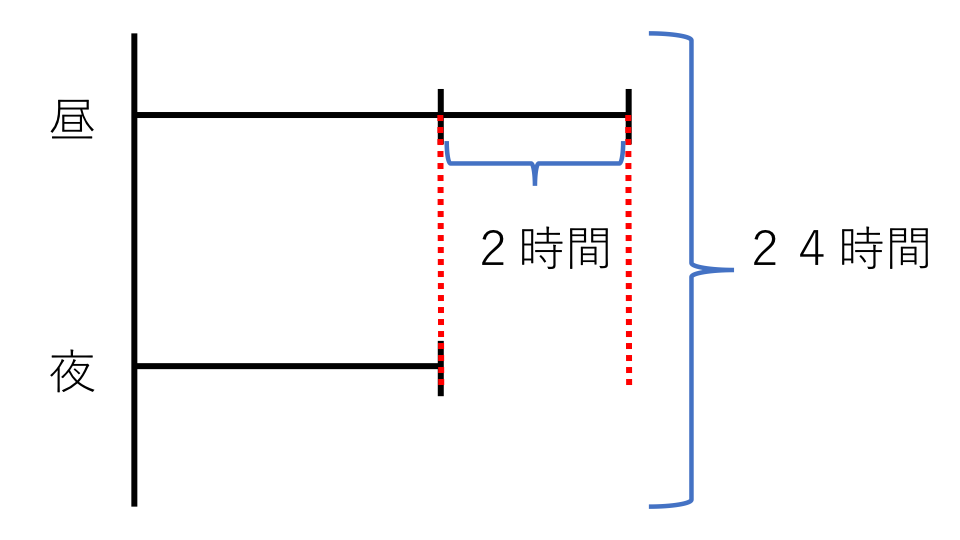
和の24に差の2を足すと全体が昼の時間の2倍になります。
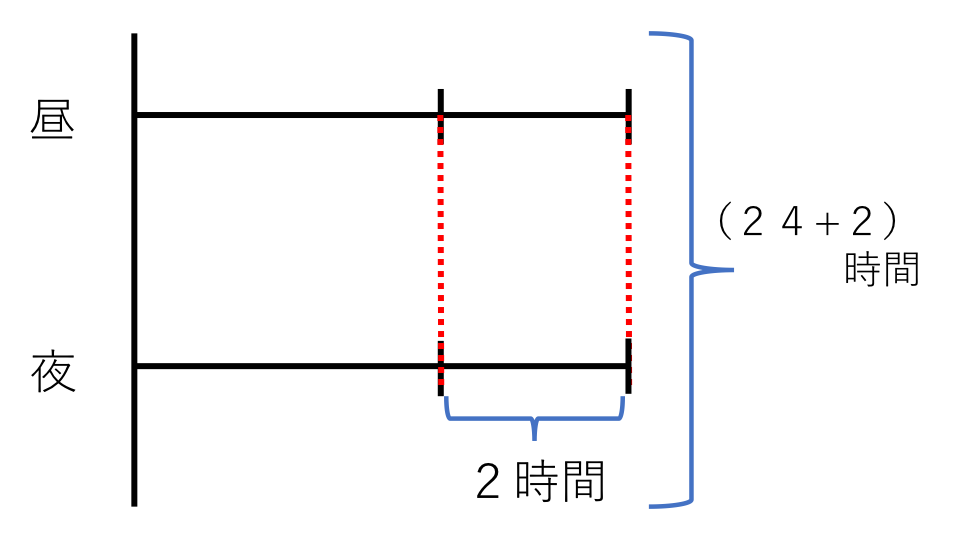
今回は全体から昼の時間を引いて求めることにします。ですので
昼の時間=(24+2)÷2=13
夜の時間=24-13=11
よって答え昼13時間、夜11時間
和差算③ 応用問題
例題4
1500円をA君、B君、C君の3人で分けます。B君はA君より100円多く、C君はA君より100円少ないとき3人の取り分け分はそれぞれ何円ですか?
解説
今回は3種類の数字が出てきました。しかしやることは変わらず、まずは全体の関係を線分図に表します。すると下の図のようになります。
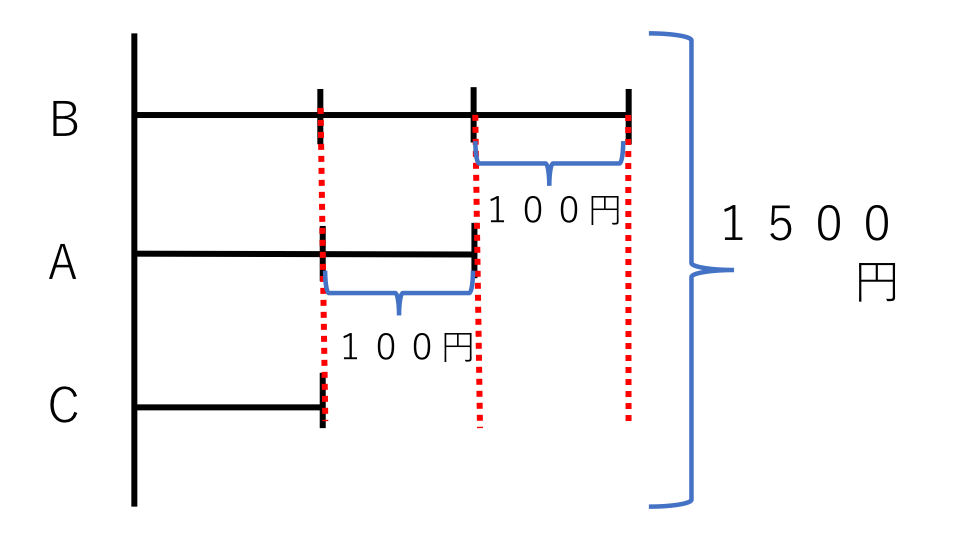
B君とC君の差額(100円+100円)とA君とC君の差額(100円)を全体の1500円からひくと、全体がC君の取分け分の3倍になります。
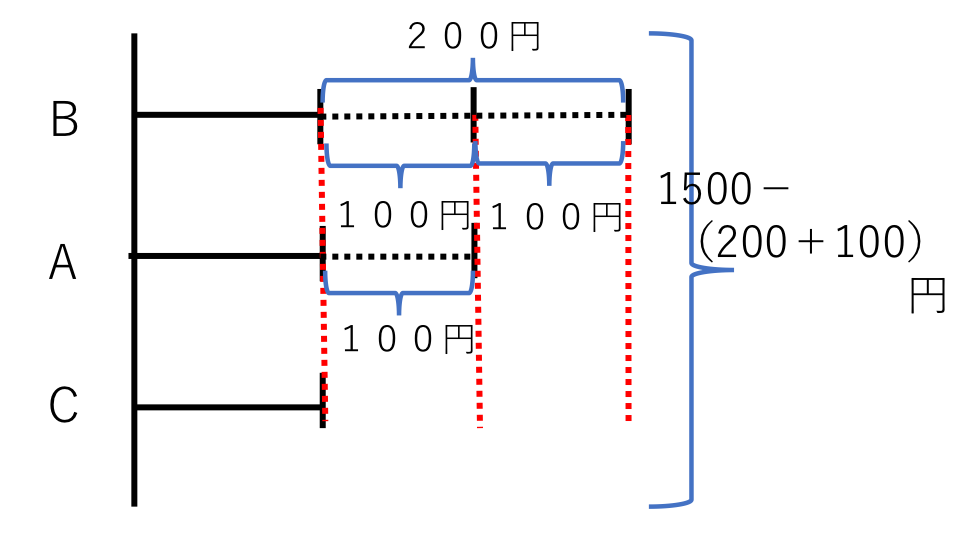
よって
C君の取分け分={1500-(200+100)}÷3=400
A君はC君より100円多いので500円
B君はC君より200円多いので600円
よって答えA君500円、B君600円、C君400円
例題5
下の図の三角形で角Aは角Bよりも13°大きく、角Cは角Aよりも35°小さい。このときの角A、B、Cの角度をそれぞれ求めなさい。
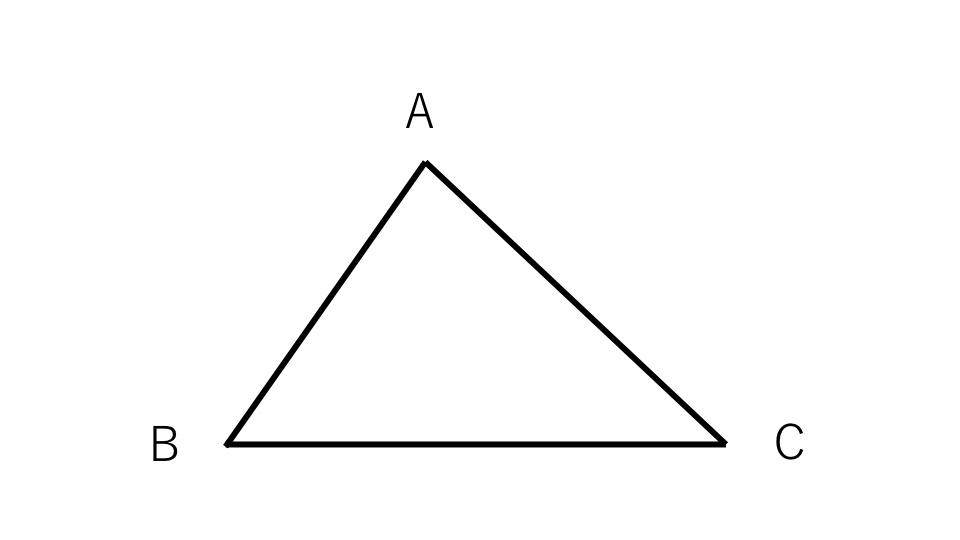
解説
まずは全体の関係を線分図に表します。
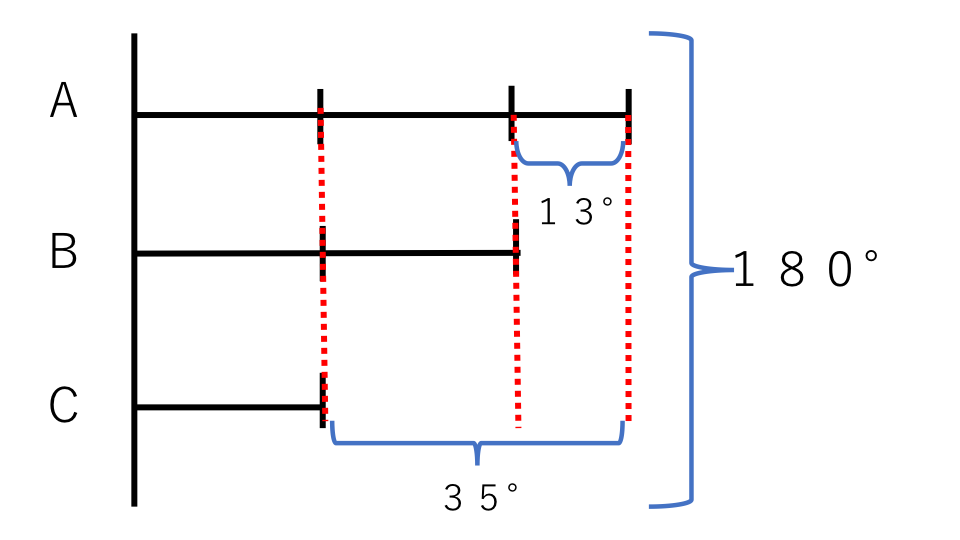
三角形の3つの和の合計は180°なので、和は180°になります。
全体から角Aと角Bの差(13°)と角Bと角Cの差(35°-13°)を足して全体(180°)からひくと全体の角度は角Cの3倍になります。
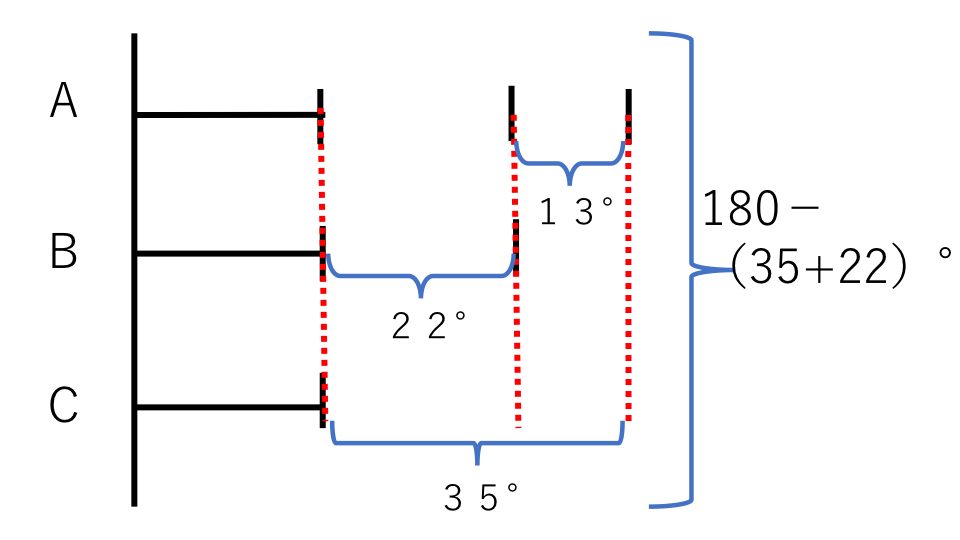
よって
角Cの角度={180-(35+22)}÷3=41°
つまり
角Aの角度=41+35=76°
角Bの角度=41+22=63°
答え角A76°角B63°角C41°
まとめ
今回の記事はいかがだったでしょうか。
線分図を書いて考えることでそこまで難しく感じなかった思います。線分図の書き方と流れを覚えてしまえば応用問題でも解くことができます。
テスト本番では必ず線分図を書いて考えるようにしましょう。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
次は過不足算のポイント解説です。和差算を理解したうえで過不足算に進むことでより理解が深まります。


