中学受験 算数 割合 ~3つの公式を使って攻略~

中学受験の算数で出題される単元「割合」。簡単に言うと、基準をもとにある量を比べたときの値を求めます。そして、中学受験で学ぶ割合は、他の単元とも関わりが深く、今後の算数、数学と学んでいく上で大変重要な単元です。小学生のうちに理解できていないと、中学生になったときに苦労します。

中学受験対策で算数の勉強をする際に最も苦労する単元の一つと言われているため、算数に苦手意識を持っている人は出来るだけ早めに対策をするべきです。

そこでこの記事では、3つの公式を使った割合の解き方を紹介します。「算数が苦手な人」「割合を初めて学習する人」「割合が苦手な人」でも理解しやすいように、わかりやすく解説しています。この記事を読むことで、割合とは何か理解でき、公式を使った解き方を効率よく取得できるようになるでしょう。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

割合① 割合とは、3つの公式

割合とは2つの数量を比べたとき、片方の数量を基準にして、他方の数量がその数量の何倍にあたるのか、もしくは何分のいくつにあたるのかを表した数のことをいいます。

割合では、基準にする数量のことをもとにする量、割合にあたる数量を比べる量といいます。これは後から公式を理解するのに必要な定義となってきますので、必ず覚えてください。

割合は、3倍、0.6(倍)、1/2(倍)などのように、整数や小数分数で表します。また百分率(%)や歩合(割、分、厘)、比を使って表す場合もあります。今回は百分率、歩合、比を使わないので別の記事で解説します。

※割合を表す数が1よりも小さい、小数や分数の場合は、倍をつけないこともあります。

具体例を用いて、今までお話しした内容を説明します。下の図を見てください。

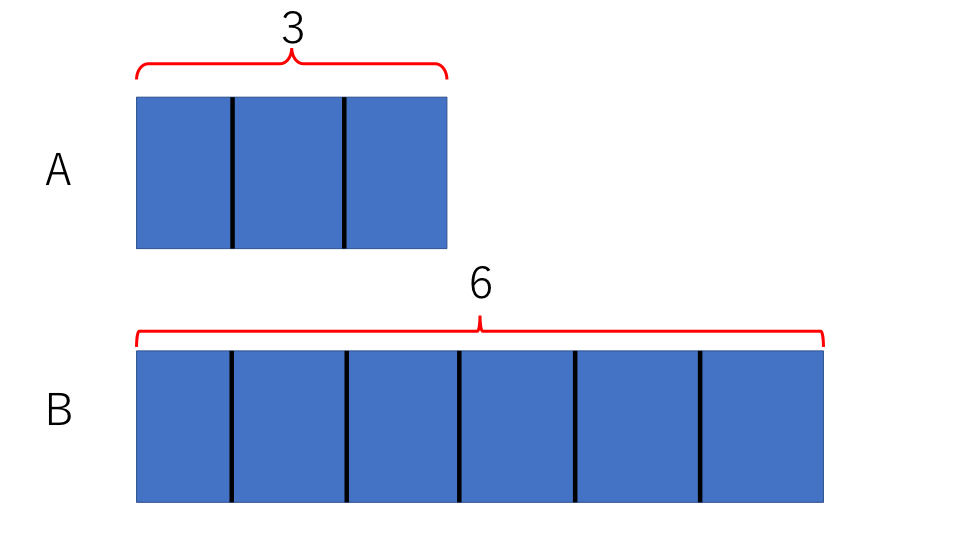
この図のどちらか一方を基準にすると、もう一方は割合を使って以下のように表すことができます。

Aを基準にした場合のBの割合は、

6÷3＝2(倍) これはBはAの2倍であることを表しています。

Bを基準にした場合のAの割合は、

3÷6＝1/2(倍) これはAはBの1/2倍であることを表しています。

割合、比べる量、もとにする量の3つの数量の関係はこのような公式で表すことができます。

公式をみてもらうと分かると思いますが、割合、比べる量、もとにする量のどれか2つがわかっていればあと1つは式で求めることができます。

式変形することで上の1つのみ暗記するだけで、残りの2つの式を導き出せますが、覚えた方が時間短縮にもなり早く解くことができるので覚えましょう。

しかし割合というものはどのようなものなのか定義をわかっていれば、簡単に式を導き出すことができます。ですので冒頭でお伝えした割合とは何か説明した部分を十分に理解しておいてください。

割合② 基本問題

例題1

あるお肉屋さんで、下の表のような値段でお肉を売っていました。

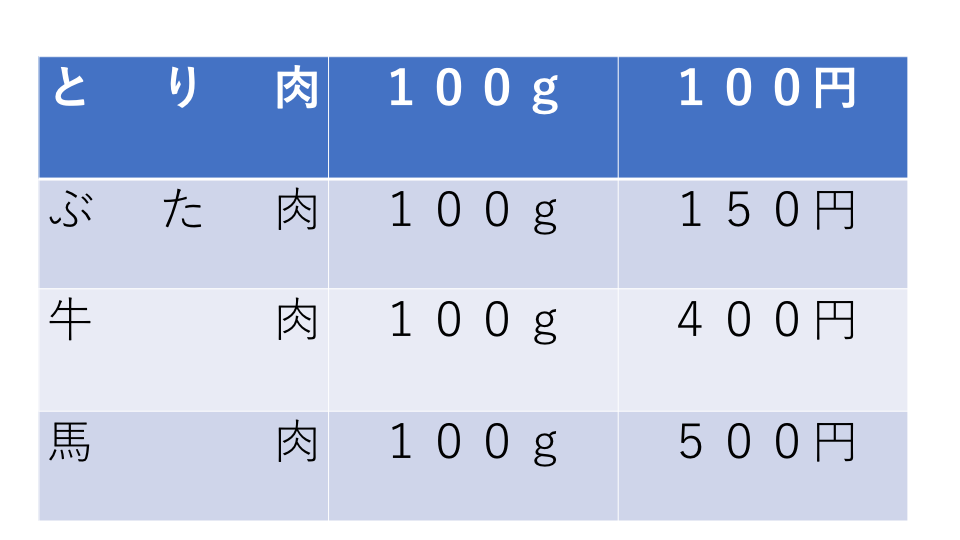
次の問いに答えなさい。

(1)とり肉の値段をもとにして、他のお肉の値段を表しなさい。

(2)馬肉の値段をもとにして、他のお肉の値段を表しなさい。

解説

(1)から解説していきます。とり肉の値段が「もとにする量」で残りのお肉が「比べる量」になります。

公式「割合＝比べる量÷もとにする量」を使って求めます。

ぶた肉は、150÷100＝1.5(倍)

牛肉は、400÷100＝4(倍)

馬肉は、500÷100＝5(倍)

よって、答え　ぶた肉1.5倍、牛肉4倍、馬肉5倍

(2)も(1)と同様に求めていきます。馬肉の値段が「もとにする量」で残りのお肉が「比べる量」になります。

とり肉は、100÷500＝0.2(倍)

ぶた肉は、150÷500＝0.3(倍)

牛肉は、400÷500＝0.8(倍)

よって、答え　とり肉0.2(倍)、ぶた肉0.3(倍)、牛肉0.8(倍)

例題2

桜さんのクラスの人数は30人です。ある日そのクラスで歯科検診があり12人が虫歯があるとわかりました。

次の割合を答えなさい。

(1)虫歯のある人は、全体のどれだけに当たるか答えなさい。

(2) 虫歯のない人は、全体のどれだけに当たるか答えなさい。

解説

(1)から解説していきます。虫歯のある人が「比べる量」、クラス全体の人数が「もとにする量」となります。公式「割合＝比べる量÷もとにする量」を使って求めます。虫歯のある人は12人、クラス全体の人数は30人なので式は、

12÷30＝0.4(倍)

よって、答え　0.4(倍)

(2)も同じようにに求めていきます。虫歯のない人が「比べる量」、クラス全体の人数が「もとにする量」となります。虫歯のない人はクラス全体から虫歯がある人の人数を引けば求めることができます。ですので、虫歯のない人は、

30-12＝18(人) となります。

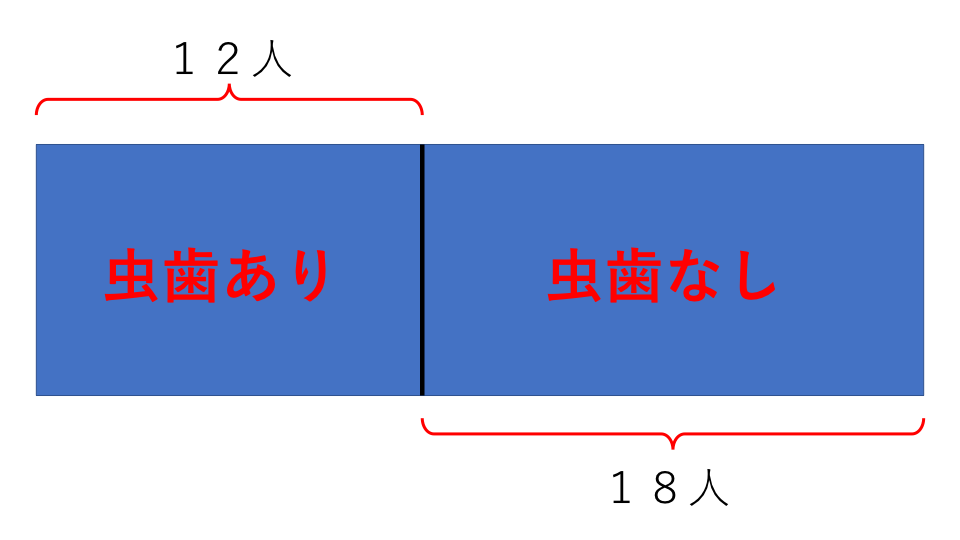
虫歯のある人は18人、クラス全体の人数は30人なので式は、

18÷30＝0.6(倍)

よって、答え　0.6(倍)

例題3

太郎さんの学校で身体検査を行いました。どこも病気がない人は全体の1/4でした。学校全体の人数は460人です。このとき病気にかかっている人は何人か求めなさい。

解説

まずは病気にかかっている人の割合を求めます。どこも病気がない人は全体の1/4です。全体を1と考えたとき、病気にかかっている人の割合は、

1-1/4＝3/4 となります。

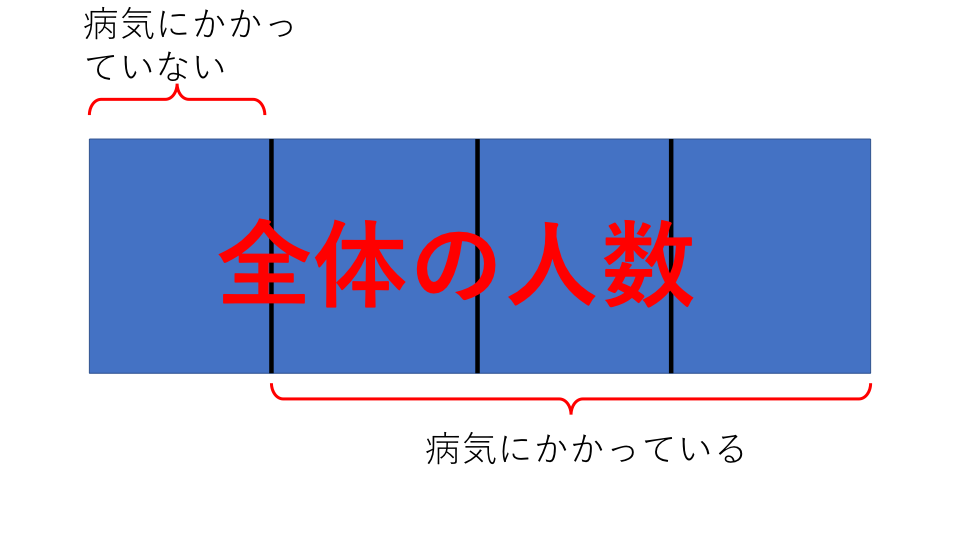
病気にかかっている人が「比べる量」、学校全体の人数が「もとにする量」になります。問題では病気にかかっている人の人数を聞いているので、この問題では「比べる量」を求めます。ですので、公式「比べる量＝もとにする量×割合」に当てはめて求めます。

460×3/4＝345(人)

よって、答え　345人

例題4

100ページの本を、1日目に全体の1/5読み、2日目に残りの3/4を読みました。あと残り何ページあるか求めなさい。

解説

まず初めに1日目時点での残りのページを求めます。

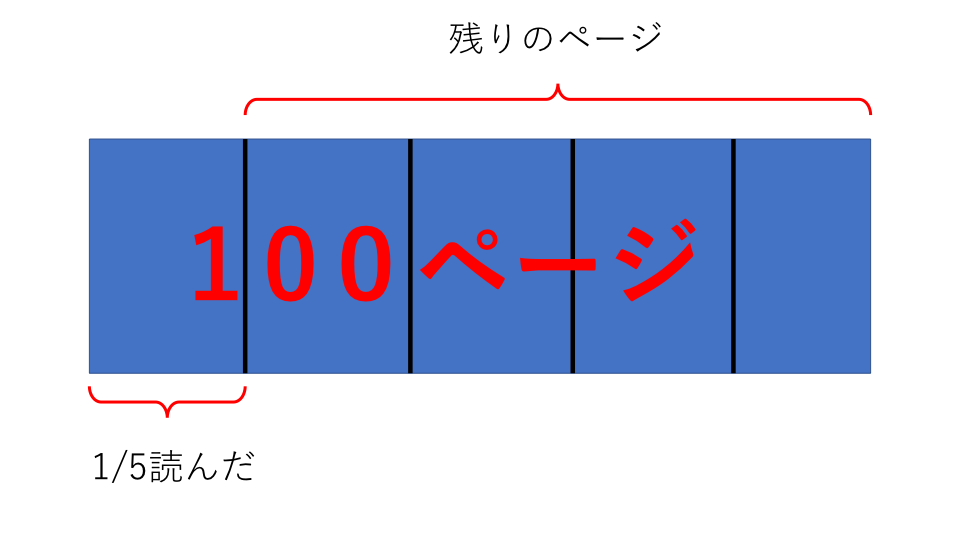
上の図のように100ページの1/5を読んだので、残りのページは4/5になります。残りのページが「比べる量」、全体のページが「もとにする量」になります。

残りのページ求める、つまり比べる量を求めたいので、公式「比べる量＝もとにする量×割合」に当てはめて考えます。ですので1日目時点での残りのページは、

100×4/5＝80(ページ) となります。

次は2日目で考えます。

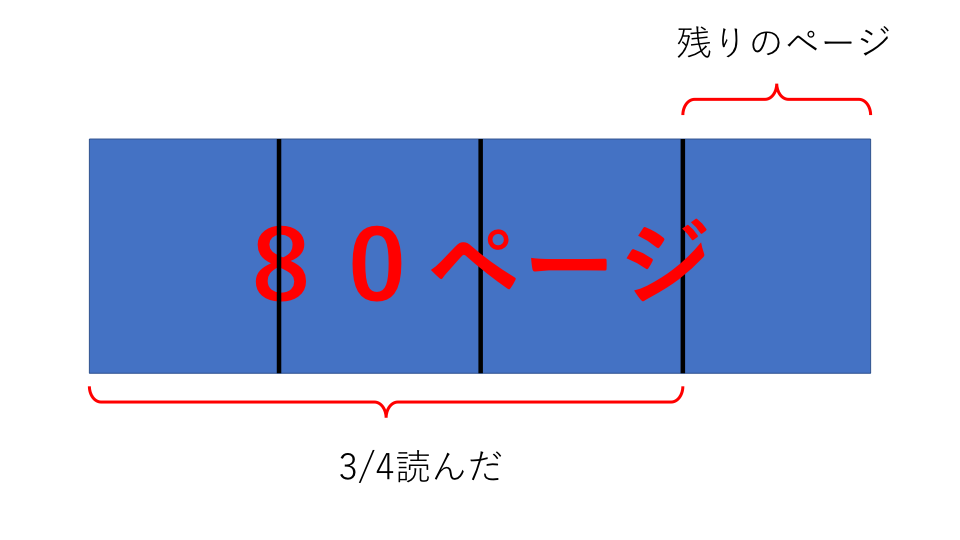
上の図のように2日目に80ページの3/4を読んだことになるので残りは80ページの1/4だとわかります。

1日目と同じように残りのページを求めると、

80×1/4＝20(ページ)

よって、答え　20ページ

このような問題のように比べる量が変化する問題も出題されるので注意しましょう。

割合③ 応用問題

例題5

桜さんはある本を、1日目に全体の2/5読み、2日目に残りの1/2を読みました。すると残りのページは45ページになりました。この本は全部で何ページあったのか求めなさい。

解説

全体1を1として考えます。すると1日目の残りのページは以下の図のようになります。

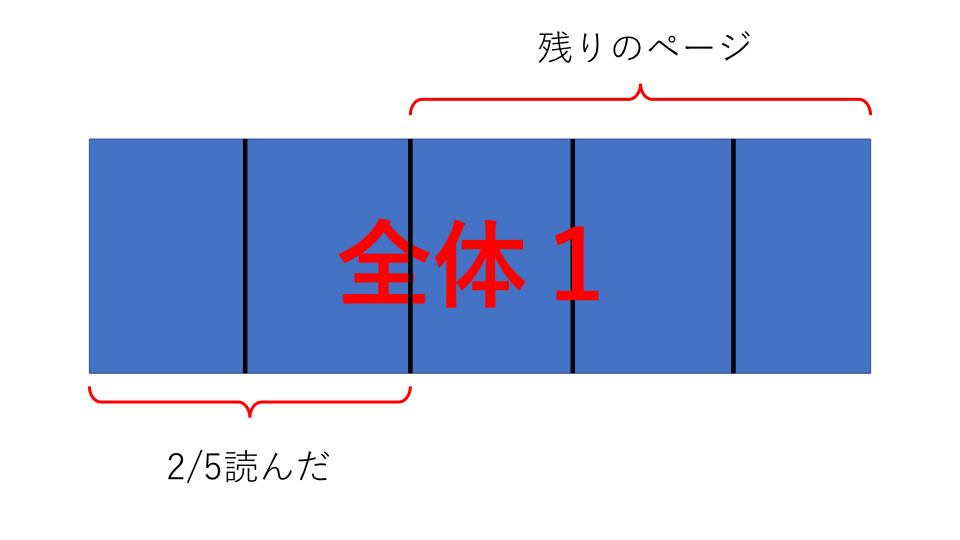
残りページは3/5となります。2日目は残りの3/5の1/2を読みました。残りページは以下の図のようになります。

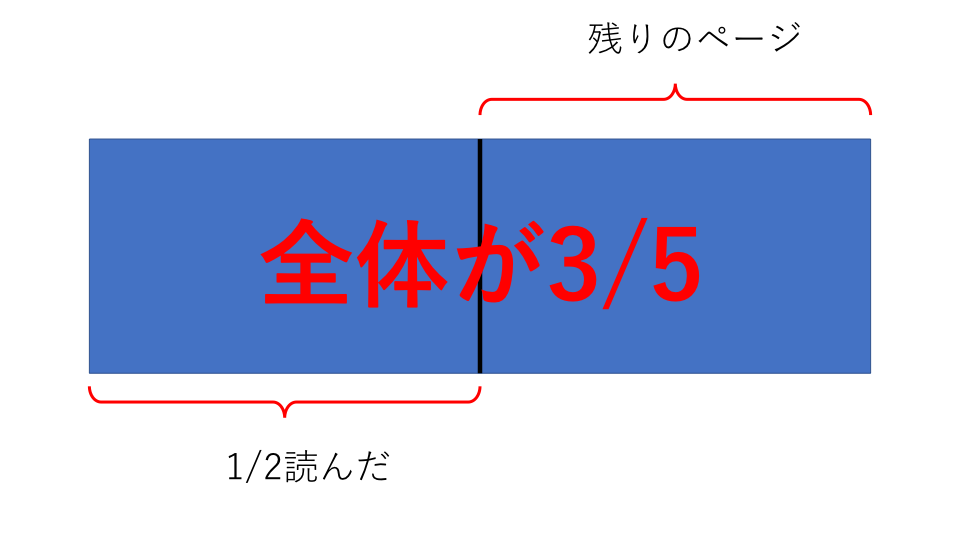
残りの3/5の1/2が45ページに値することがわかります。つまり全体の(3/5×1/2＝3/10)が45ページということになります。

元にする量を求めたいので、公式「もとにする量＝比べる量÷割合」を使って本のページ数を求めると式は、

45÷3/10＝150(ページ)

よって、答え　150ページ

例題6

特製の照り焼きソースを作ることにしました。醤油を5、砂糖を3、みりんを2の割合で混ぜて作ります。みりんを100g用意しました。このとき醤油と砂糖をどれだけ用意する必要がありますか。

解説

それぞれの割合から、まずは全体の割合を計算します。それぞれの割合が5、3、2なので5＋3＋2＝10なり、みりんの全体に対する割合は2/10、醤油は5/10、砂糖は3/10となります。　

元にする量を求めたいので、公式「もとにする量＝比べる量÷割合」を使って全体の重さを求めると、

全体の重さは100÷2/10＝500(g)となります。

全体の重さがわかったので、そこから各割合をかけて各重さを求めることができます。

醤油は、500×5/10＝250(g)

砂糖は、500×3/10＝150(g)

よって、答え　醤油250g、砂糖150g

まとめ

いかがだったでしょうか？公式を覚えて文章で示されている数量がどの量になるのかわかれば簡単に解けることがわかってもらえたと思います。また応用問題では全体の量を考えることができれば解くことができます。もしわかりずらかったら、今回の解説で示したように図形を書いて考えると理解しやすいと思います。

次は損益算のポイント解説です。割合を理解したうえで損益算に進むことでより理解が深まります。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】