中学受験の算数で出題される単元「仕事算」。中学受験以外にも公務員試験やSPI試験などにも出題されます。そのため、受験だけでなく将来のことも考えると、とても大切な単元だと言えます。
中学受験の算数で出るこの問題の特殊な点は、問題によって仕事の量が違ったり、複数の管で水槽を満たす水槽算と様々なパターンが存在します。点数にばらつきがあったり、解ける問題と解けない問題があるのではないでしょうか?
しかし、どんなパターンが出題されたとしても、大切なポイントさえ抑えておけば苦戦することはありません。今のうちに重要なポイントを抑えて、仕事算の問題を得点源にしていきましょう。
この記事では、3パターンの解き方を使って解説しています。この記事を読むことで自分の解き易い方法を見つけることができます。数学が苦手な人でもわかりやすく解説しているので、仕事算が得意になること間違いありません。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
仕事算とは?
仕事算とは複数人で仕事をするのにかかる時間を求める問題のことを言います。よく出る問題を3つご紹介します。
二人で協力して仕事をする問題
ある仕事を行うために太郎くんは5時間、花子さんは3時間かかります。このとき太郎くんと花子さんが一緒に行うとどれだけの時間で終えることができますか?
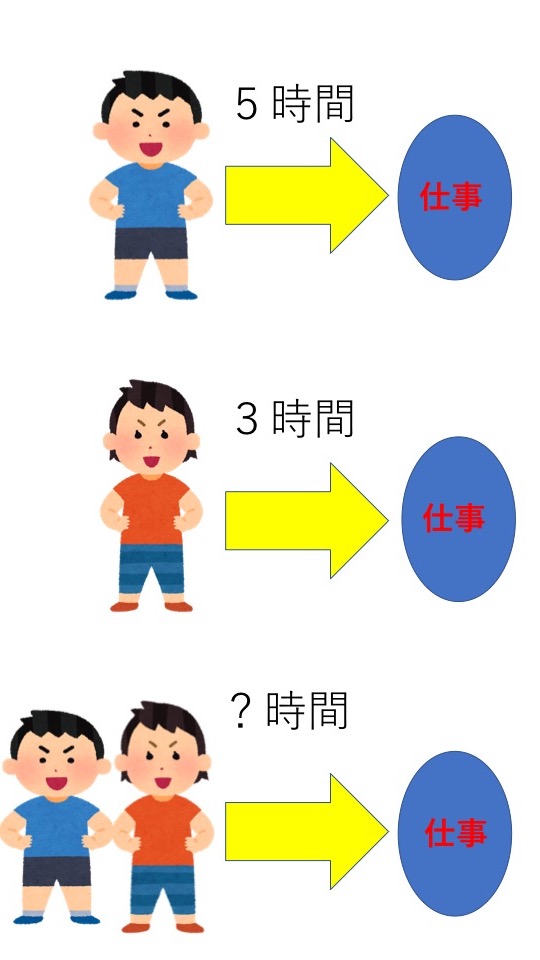
途中から仕事をする人が変わる問題
ある仕事を行うために太郎くんは5時間、花子さんは3時間かかります。太郎くんだけが仕事を2時間だけして残りを花子さんがする場合、花子さんはどれだけの時間がかかりますか?

2本の管で水そうを満たす問題
ある水そうを水で満たすために4時間かかるA管と5時間かかるBの管がある。空の水そうにはじめA管とB管の両方を用いて1時間入れた後、A管だけを用いて水そう満タンまで入れた。A管だけで水を入れ始めてから水を満たすのに何分かかりましたか?
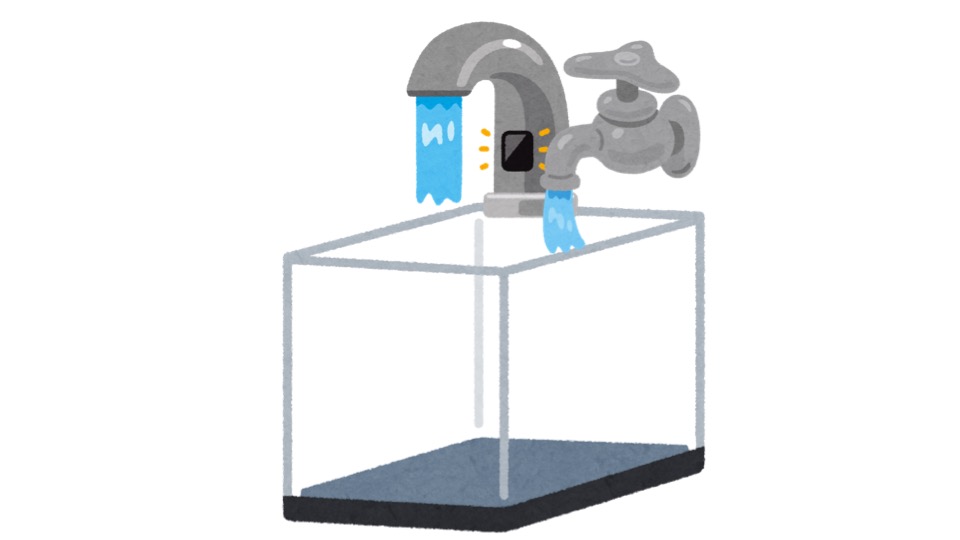
このような問題がよく出題されます。一見、それぞれが違う問題に見えますが、根本的な考え方は同じで、重要なポイントを抑えれば、難しい問題ではありません。今からご紹介する3パターンの解き方をマスターして仕事算を得意にしてください。
3パターンの解き方
先程例にも示した問題を3パターンのやり方で解いていきます。3パターン解き方をご紹介しますが、まずは「仕事量」を決めることが大切です。
例題1
ある仕事を行うために太郎くんは5時間、花子さんは3時間かかります。このとき太郎くんと花子さんが一緒に行うとどれだけの時間で終えることができますか?
全体の仕事量をそれぞれの「最小公倍数」で決める
太郎くんと花子さんが仕事を終えるために必要な時間はそれぞれ5時間と3時間です。これらの数字5と3の最小公倍数は15なので、全体の仕事量を「15」と決めます。少しわかりづらいので、具体的に「15枚の折り紙を作る」、「15個のおにぎりを作る」などと考えてイメージしてください。
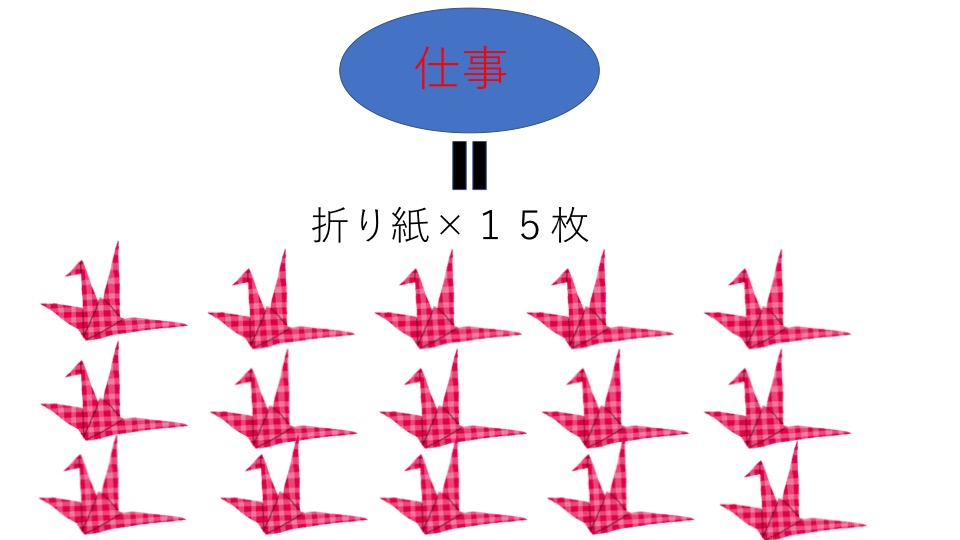
仕事量を決めることで「単位時間あたりの仕事量」が決まります。
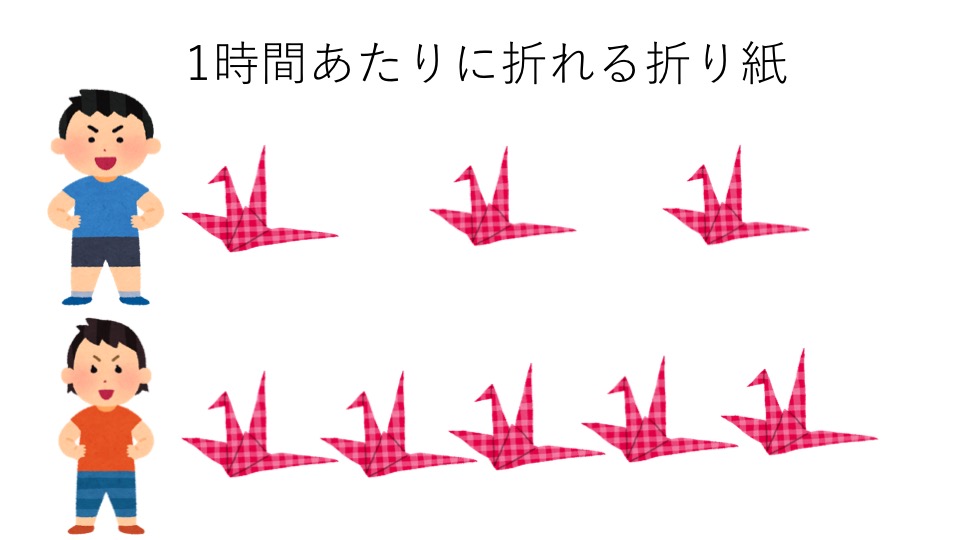
- 太郎さん:1時間で3枚の折り紙が折れる(15枚の折り紙が5時間で折れる)
- 花子さん:1時間で5枚の折り紙が折れる(15枚の折り紙が3時間で折れる)
- 二人合わせて:1時間で8枚の折り紙が折れる。
全体の仕事量を最小公倍数にするのは、仕事の値が整数になるからです。
このように考えられると「1時間で8枚の折り紙が折れる場合、15枚の折り紙を折るのにどれくらいの時間がかかりますか?」という問題に置き換えて考ればいいです。ですので式は以下の通りになります。
15÷8=1.875(時間)
小数点以下の0.875を「分」直すと
0.875×60=52.5(分)
小数点以下0.5を「秒」直すと
0.5×60=30(秒)
つまり答えは1時間52分30秒となります。
全体の仕事量を「1」として考える
先程は全体の仕事量を最小公倍数で決めましたが、今回は1と考えて解いていきます。
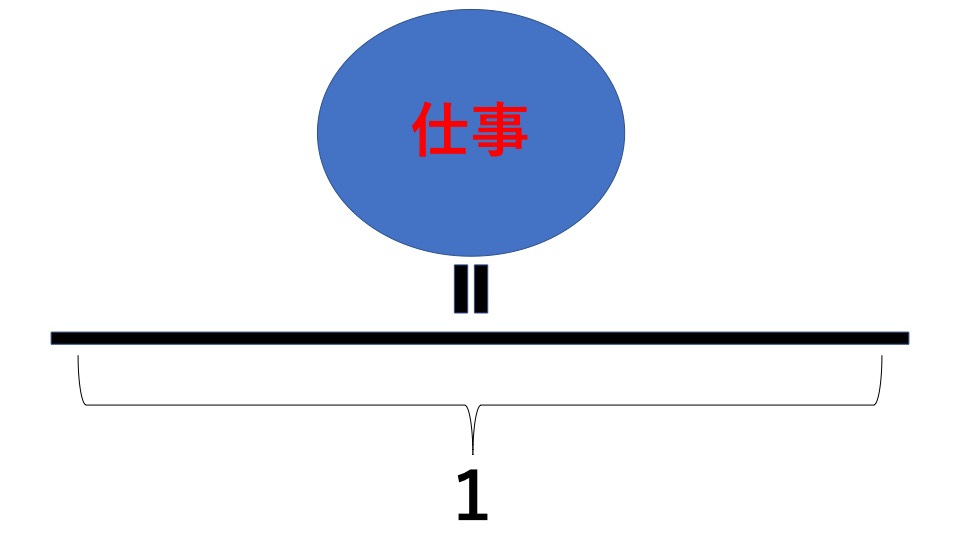
全体の仕事量を1として考えた場合のそれぞれの単位時間あたりの仕事量は
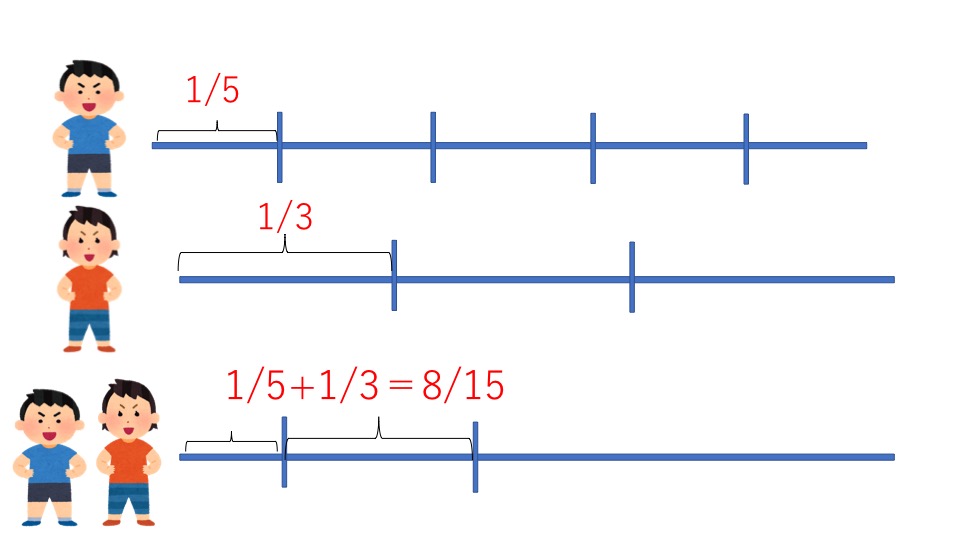
- 太郎さん:1時間あたり1/5
- 花子さん:1時間あたり1/3
- 二人合わせて:1時間あたり8/15(1/5+1/3)
ここまで考えることができると「1時間で全体の8/15の仕事ができる場合、仕事を終えるのにどれくらいの時間がかかりますか?」と問題を言い換えることができます。全体の仕事量は1ですので式は
1÷8/15=15/8=1.875(時間)
答え1時間52分30秒 となります。
1人の単位時間あたりの仕事量を「1」として考える
これまでは全体の仕事量を最小公倍数や1として考えてきました。今度は太郎さんもしくは花子さんの単位時間あたりの仕事量を「1」と決めます。今回は太郎さんの単位時間あたりの仕事量を1とし「1枚の折り紙を折る」と考えてください。
そうすると全体の仕事量は「5枚の折り紙を折る」というふうになります。
それぞれの単位時間あたりの仕事量は

- 太郎さん:1時間あたり1枚の折り紙を折ることができる
- 花子さん:1時間あたり5/3枚折り紙を折ることができる
- 二人合わせて:1時間あたり8/3(1+5/3)枚折り紙を折ることができる
ここまで考えることができると「1時間で8/3枚折り紙を折ることができる場合、5枚の折り紙を折るためにはどれくらいの時間がかかりますか?」と問題を言い換えることができます。ですので式は
5÷8/3=15/8=1.875(時間)
答え1時間52分30秒 となります。
仕事算のポイント
このように3パターンの解き方がありますが、基本的な考え方は同じです。
- 「仕事量」を決める
- 決めた仕事量からそれぞれの「単位時間あたりの仕事量を求める」
この2つのポイントは必ず覚えてください。問題によってどのやり方で解くのが最適かというのは変わってくるので、どのやり方でも解けるようにしてください。
しかし基本的には全体の仕事量をそれぞれの「最小公倍数」で決めるやり方がオススメです。なぜなら値が整数になり、なおかつイメージしやすいからです。
それでは一番初めの例として挙げた問題で練習してみましょう。
仕事算の練習問題
練習問題1
ある仕事を行うために太郎くんは5時間、花子さんは3時間かかります。太郎くんだけが仕事を2時間だけして残りを花子さんがする場合、花子さんはどれだけの時間がかかりますか?
解説
今回は全体の仕事量を「最小公倍数」で決めていきたいと思います。そうする太郎くんと花子さんが仕事を終えるために必要な時間はそれぞれ5時間と3時間です。これらの数字5と3の最小公倍数は15なので、全体の仕事量を「15」と決めます。
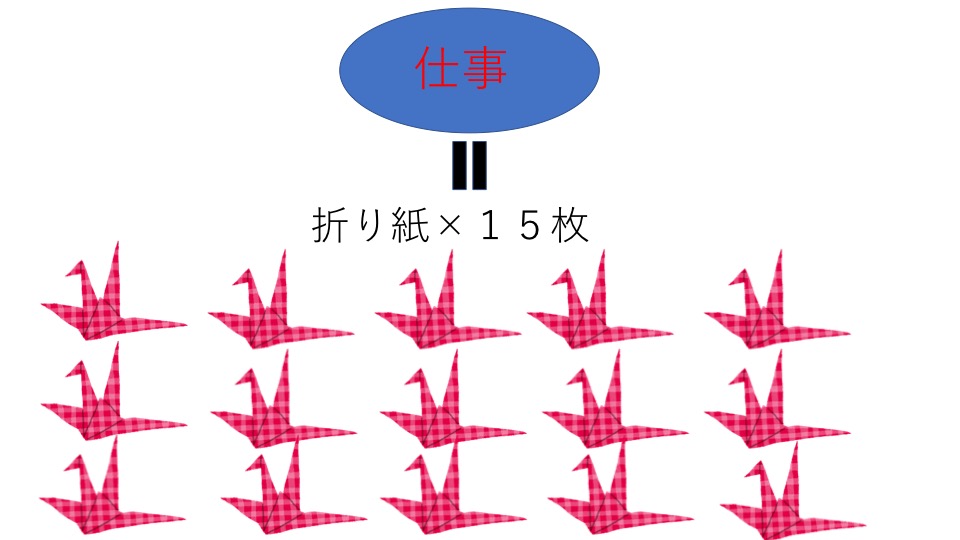
仕事量を決めることで「単位時間あたりの仕事量」が決まります。
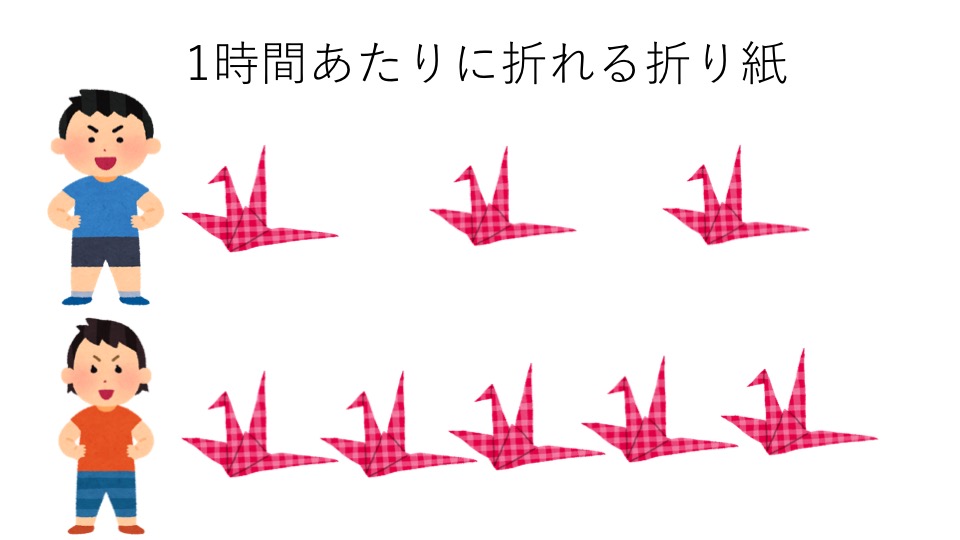
- 太郎さん:1時間で3枚の折り紙が折れる
- 花子さん:1時間で5枚の折り紙が折れる
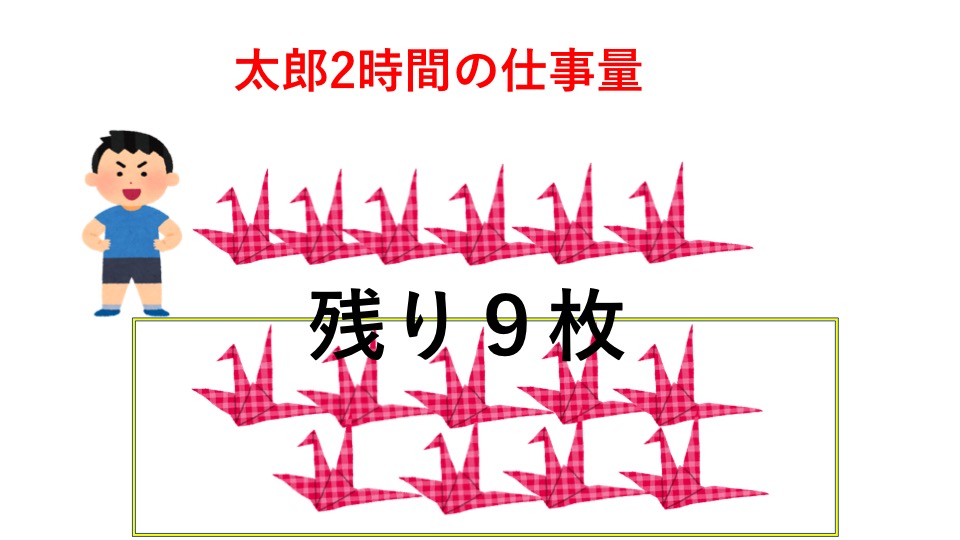
ここで太郎さんは2時間だけ仕事をしたので、折った折り紙の枚数は6枚で残りは9枚となります。ここまで考えることができると「花子さんは1時間で5枚の折り紙を折ることができます。9枚折るのにどれくらいの時間がかかりますか?」と言い換えることができます。ですので式は
9÷5=1.8(時間)
小数点以下0.8を「分」に直すと
0.8×60=48(分)
よっては答えは1時間48分となります。
練習問題2
ある水そうを水で満たすために4時間かかるA管と5時間かるBの管がある。空の水そうにはじめA管とB管の両方を用いて1時間入れた後、A管だけを用いて水そう満タンまで入れた。A管だけで水を入れ始めてから水を満たすのに何分かかりましたか?
解説
今回は全体の仕事量を「1」として考えます。
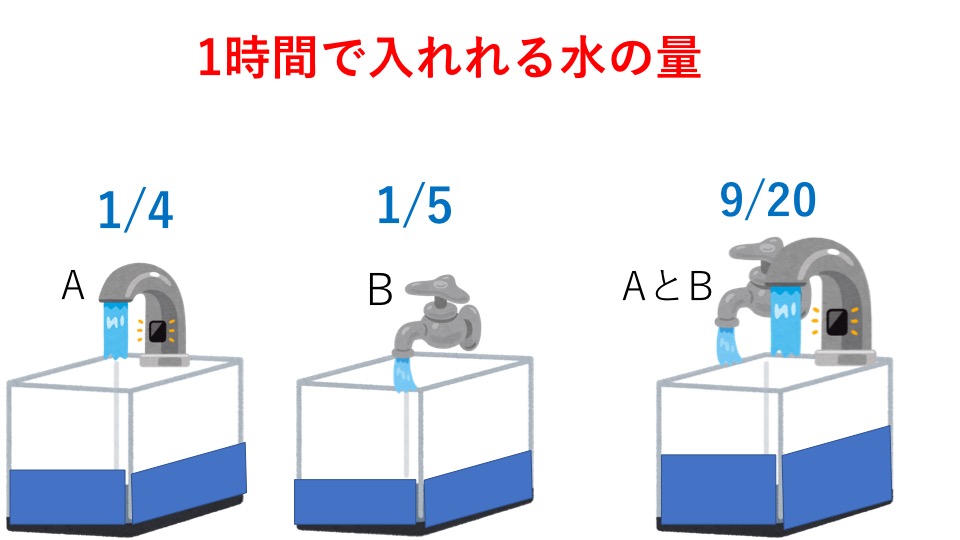
上の図のようになり、それぞれの単位時間あたりの水の量は以下のようになります。
- A管:1時間で入れる水の量は1/4
- B管:1時間で入れる水の量は1/5
- A管とB管合わせて:1時間で入れる水の量は9/20
初めはA管とB管両方を用いて1時間入れたので残りは11/20となります。ここまで考えることができると「1時間で1/4の水を入れることができるA管がある。11/20入れるためにはどれくらいの時間がかかりますか?」と言い換えることができます。ですので式は
11/20÷1/4=11/5=2.2(時間)
小数点以下0.2を「分」に直すと
0.2×60=12(分)
よって答え2時間12分となります。
まとめ
いかがだったでしょうか?3パターンのやり方をご紹介しましたが、どのやり方も共通して仕事量を決めることが大切だと感じてもらえたと思います。
仕事算の問題は一番初めに仕事量を決めることが最も重要なポイントです。このことが十分に理解できていれば、どんなに難しい問題が出題されても正解することができると思います。
最後までご覧いただきありがとうございました。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

