中学受験 算数 計算問題で計算ミスをなくす正しい工夫の仕方

中学受験の算数で必ずと言ってよいほど出題される単元「計算問題」。正しく正確に計算できるかどうかが求められます。中学受験算数の計算問題はライバルに差をつけられないためにも、確実に点を取っておきたい単元です。

ただし計算問題はその性質からケアレスミスをする人が多い単元でもあり、そういった計算ミスをなくすことが算数は確実に得意教科にするための第一歩です。早い時期に計算力を身につけることが今後の算数の伸びに大きく関わってくるので、必ず計算力は身につけておきましょう。

算数の計算でよく間違える人、ケアレスミスをよくしてしまう人、計算の工夫の仕方を知りたい人は、この記事を読むことで、計算の正しいやり方が身につき計算問題で失点しにくくなるはずです。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

さくらんぼ計算

よく2ケタ＋2ケタ足し算で計算ミスをしてしまうことが多いのではないでしょうか？繰り上がりのある計算になった途端に、指を曲げたり開いたりして考えていませんか？この考え方は悪くはないのですが、時間制約のある中学受験では時間が足りなくなってしまいます。

そこでオススメするのが「さくらんぼ計算」です。まずはどのような方法か説明します。下の図を見てください。

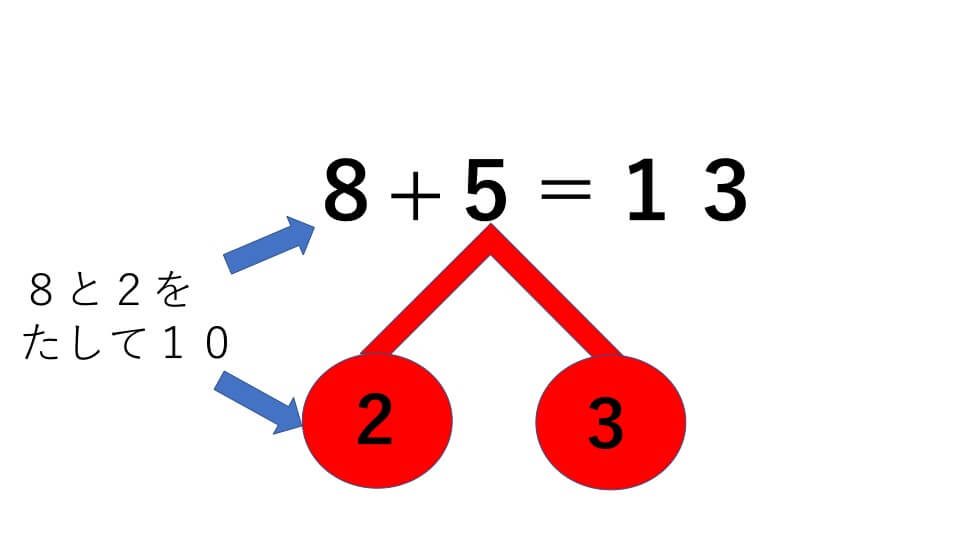
1. 5の下にさくらんぼを描き、5を2と3に分けて中に書きます。
2. 8と2をたして10
3. 10とさくらんぼの残りの3をたして、答えは13

この3ステップで解くのが「さくらんぼ計算」です。しかし、「5を2と3に分けて考える」ところで少しつまずくのではないでしょうか？「5を2と3に分ける」ためにはまず、「8と何をたしたら10になるのか」はじめに考える必要があります。

繰り上がりのある計算問題を得意にするためには、この「たして10になる数」を瞬時に言えるようになる必要があります。繰り上がりのある計算で間違いが多い子は「たして10になる数」が瞬時に言えないことが多い場合があります。ですので「たして10になる数」がすぐに言えるようになるまで練習をしましょう。

たし算

「さくらんぼ計算」の考え方を使うことで2ケタ＋1ケタや2ケタ＋2ケタの計算もできるようになります。次の例をそれぞれ見てください。

例題1

78＋5＝

解説

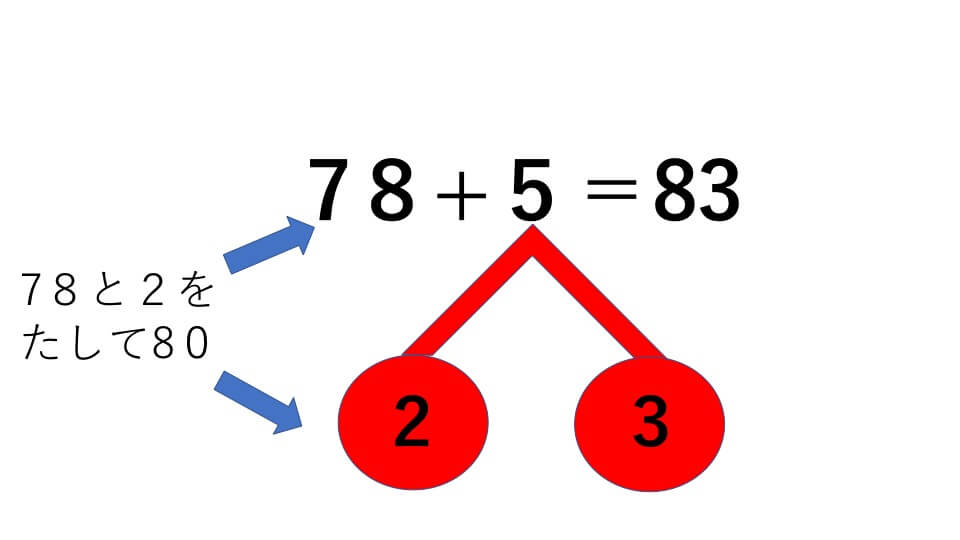
1. 5の下にさくらんぼを描き、5を2と3に分けて、中に書きます。
2. 78と2をたして80
3. 80とさくらんぼの残りの数をたして、答え83

例題2

58＋33＝

解説

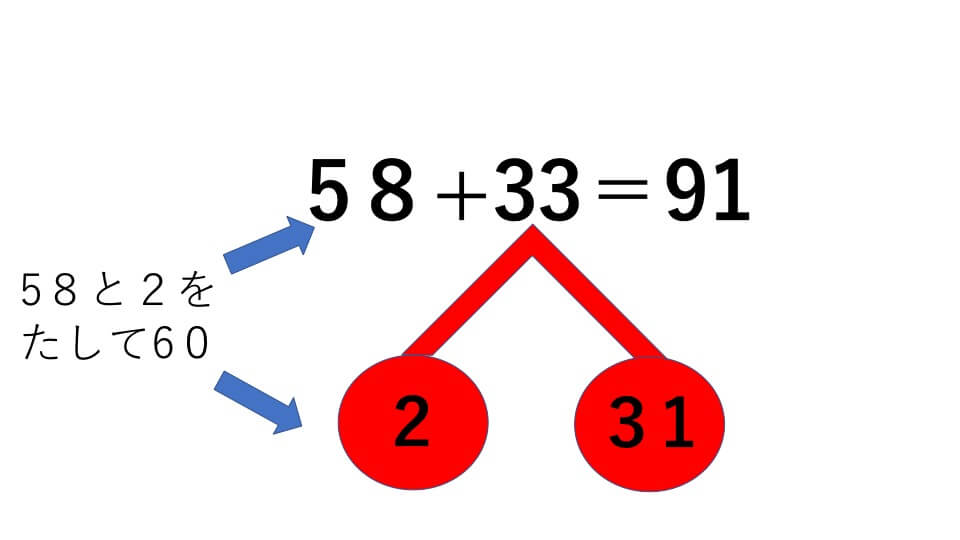
1. 33の下にさくらんぼを描き、33を2と31に分けて、中に書きます。
2. 58と2をたして60
3. 60とさくらんぼの残りの数をたして、答え91

引き算

また繰り上がりのある引き算の問題も同じように「さくらんぼ計算」を使って求めることができます。

例題3

17-9＝

解説

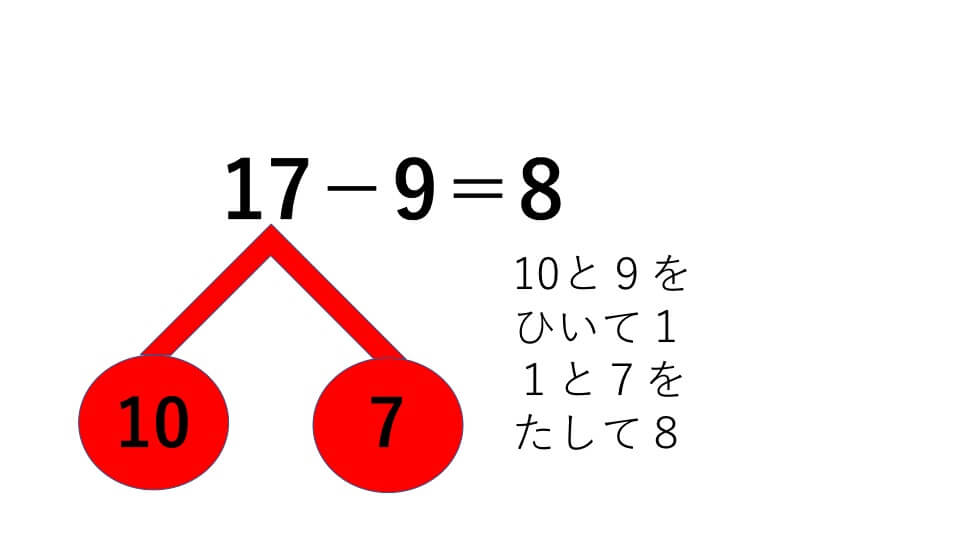
1. 15の下にさくらんぼを描き、17を10と7に分けて中に書きます。
2. 10から9を引いて1
3. 1と7をたして、答え8

この3ステップで解きます。足し算の時よりも少しややこしいと感じたと思います。「いったん引いてからたす」という考え方は確かに難しいと思います。引き算の場合は「引いてからたす」と覚えてください。ですので「引いてたすさくらんぼ計算」と覚えるといいでしょう。

また次のように考えることもできます

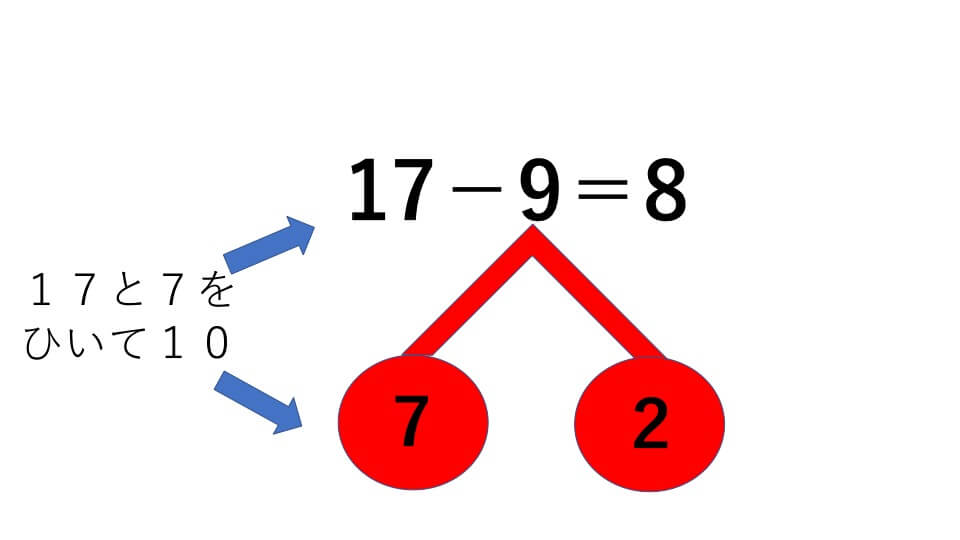
1. 9の下にさくらんぼを描き、9を7と2に分けて中に書きます
2. 17から7を引いて10
3. 10から2を引いて、答え8

こちらの方法の方が「引いてから引く」考え方なのでわかりやすいと思います。

もう少し数の大きい問題で計算してみます

例題4

85-8＝

解説

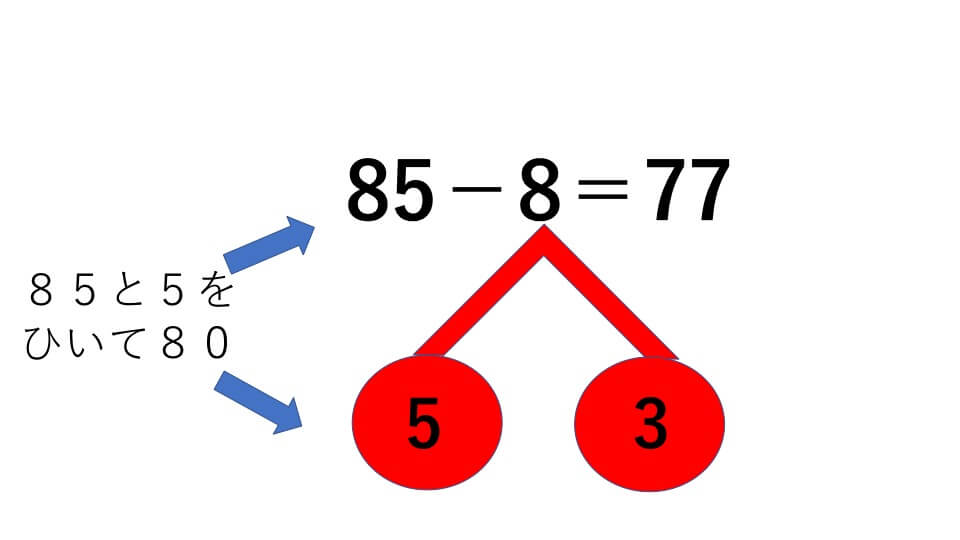
1. 8の下にさくらんぼを描き、5と3に分けて中に書きます。
2. 85から5を引いて80
3. 80から3を引いて、答え77

このように「さくらんぼ計算」は足し算だけじゃなく、2ケタ-1ケタの計算問題でも使うことができます。

今回はわかりやすくようにさくらんぼを描いていましたが、慣れてきたら頭の中でさくらんぼを書いて、暗算でできるようになるまで練習を繰り返ししてください。また引き算にさくらんぼ計算を使う時やり方は2種類ありますが、自分のやり易い方を選んでください。

おみやげ算

おみやげ算とは十の位が同じ数の2ケタの数どうしのかけ算に使える計算方法です。具体的にどのように計算をするのか説明していきます。

例題5

18×14＝

解説

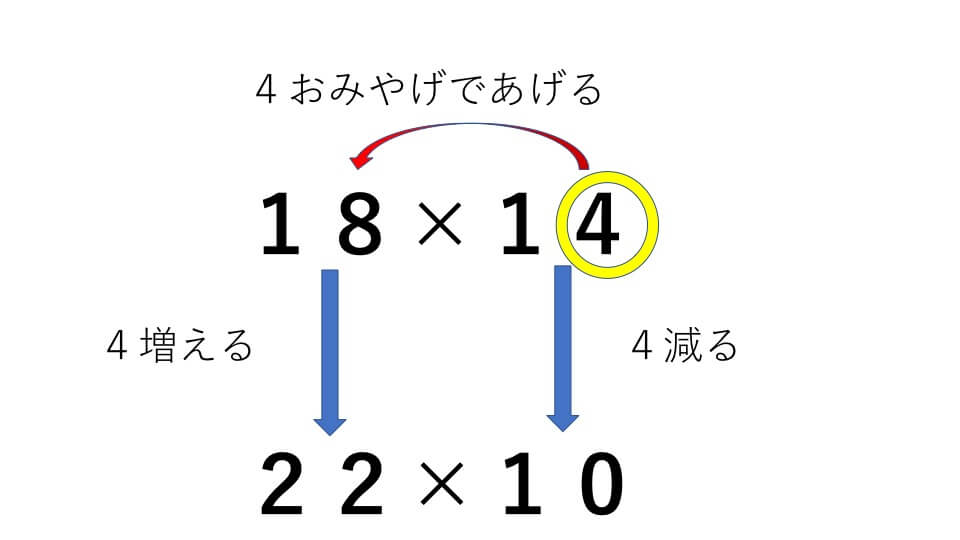
• 18×14の右の「14の一の位の4」をおみやげとして、左の18にあげます。そうすると18×14が22×10となります。
• 22×10を計算して220となります。
• その220に「18の一の位の8」と「おみやげであげた4」をかけた32をたして答え252

すごく簡単ですよね。このやり方をマスターすれば十の位が同じ数の2ケタの数どうしのかけ算が暗算で解けるようになります。もう少し大きい数字で解いてみます。

例題6

82×83＝

解説

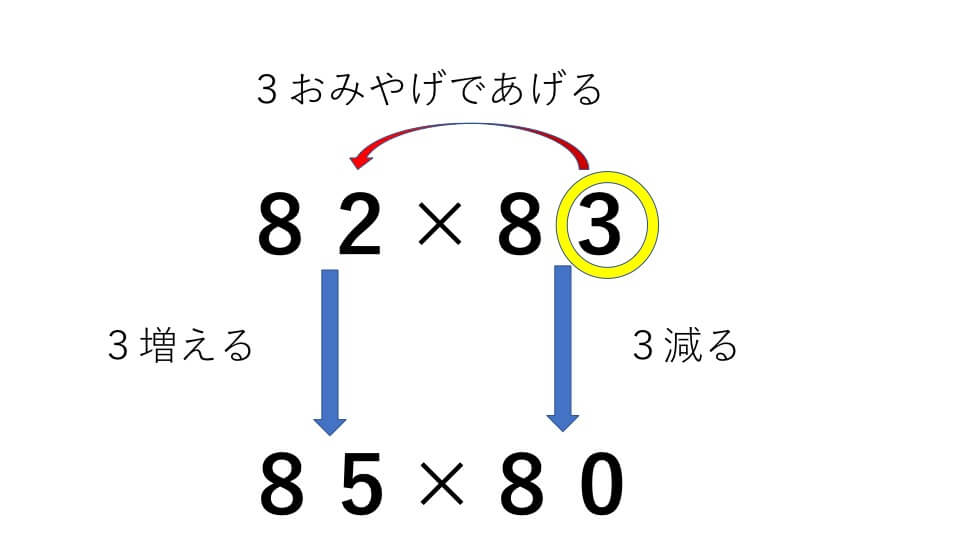
• 82×83の右の「83の一の位の3」をおみやげとして、左の82にあげます。そうすると82×83は85×80となります。
• 85×80を計算して6800となります。
• その6800に「82の一の位の2」と「おみやげであげた3」をかけた6をたして答え6806になります。

是非このやり方をマスターして大きい数字のかけ算を得意にしてください。

切りのいい数字を作って工夫する問題

例題7

58＋17＋13＋62＝

解説

いきなり計算するのではなく、まずは式全体を見てちょうど切りのいい数字を作ることができないか確認します。58と62、17と13をたすと切りのいい数字になりそうですよね。なのでその二つを先に計算して、出てきた答え同士をたす。下の図のようになります。

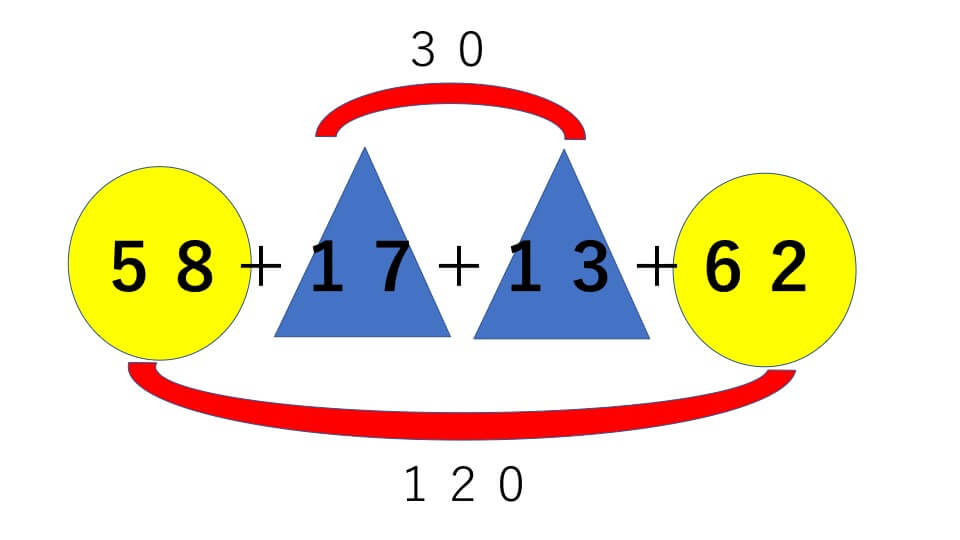
よって答え150

例題8

10＋20＋30＋40＋50＋60＋70＋80＋90＋100

解説

10と90、20と80、30と70と言うふうに組み合わせていくと100いくつかできます。

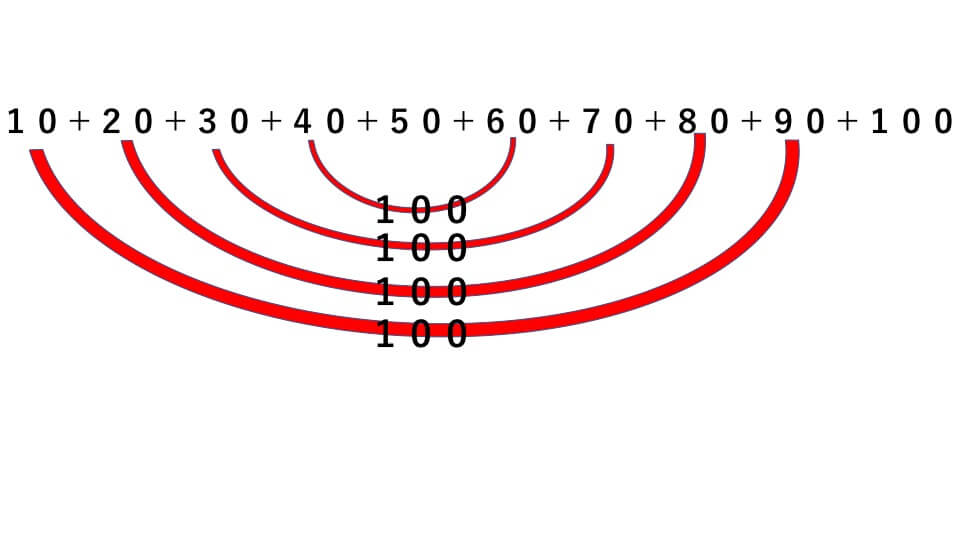
このように100が4つできます。そして残りは50と100なので

100＋100＋100＋100＋100＋50＝550となります。

このような問題のように切りのいい数字を見つけてそれらを優先して解くという工夫ができれば計算がラクになるだけではなく、計算ミスを減らすことができます。

分配法則を利用して解く問題

分配法則とは何か知らない人に説明します。分配法則とは以下のように計算を行うことです。

まずはこの法則を十分に理解した上で次の問題を解いてください。

例題9

75×22＋75×38＝

解説

まず式を見た時に、共通な数がないか確認します。共通な数がある場合は分配法則を利用して計算します。今回は75が共通な数なので、次のように分配法則を利用します。

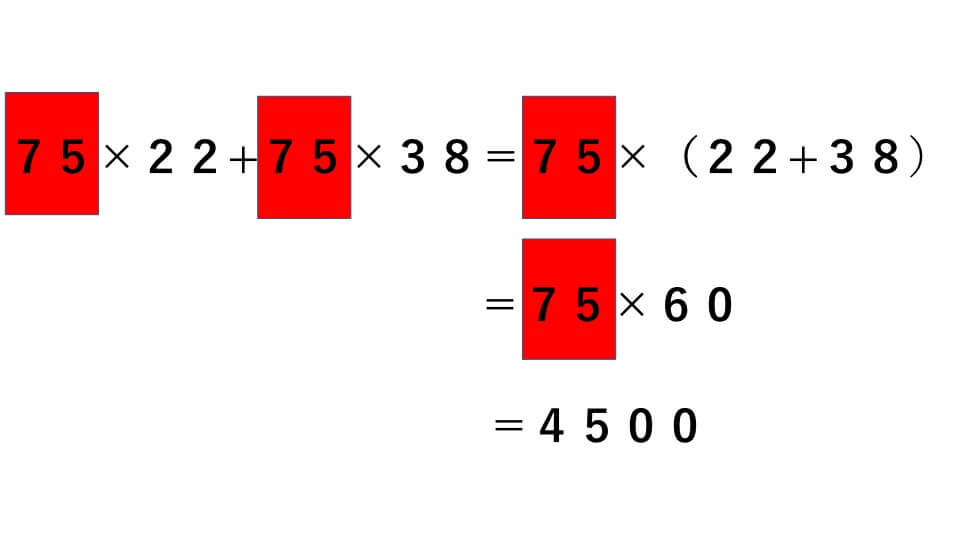
よって答え4500

例題10

0.75×45＋0.45×45＋0.8×45＝

解説

まず式を見た時に、共通な数がないか確認します。共通な数がある場合は分配法則を利用して計算します。今回は45が共通な数なので、次のように分配法則を利用します。

よって答え90

これらの問題のように式中に同じ数字が何度も出てきた場合は分配法則を利用する計算を疑うといいでしょう。

まとめ

中学受験の計算問題は正しく工夫すれば間違えることは少なく、簡単に計算できると実感してもらえたと思います。ただし、計算問題を得意にするためには、ある程度の数をこなすことは必ず必要になってきます。

まずは今回お伝えした内容を十分に理解して、お手持ちの参考書や問題集で計算問題を解いてみましょう。以下の記事では、計算問題のおすすめ問題集も紹介しています。

このように多くの計算問題に触れることで、計算自体に慣れていき、暗算力も身につけていきましょう。最後までご覧頂きありがとうございました。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】