中学受験 算数 還元算 ~逆算のやり方から詳しく解説~

中学受験の算数で出題される単元「還元算」。還元算はわからない数字を□として、問題文に沿って式をつくり、逆算して求める問題です。

還元算自体は中学受験の時だけ使い、中学校からはxを使った考え方になります。

しかし、還元算の考え方は大学受験まで使う考え方なので、今のうちに十分に理解しておく必要があります。還元算を理解できると、今後の算数の文章問題で苦戦することは少なくなるでしょう。これから出題される文章問題を考える上での基礎となります。

この記事では、還元算のやり方を解説していき、「算数が苦手な人」「還元算を初めて学習する人」「還元算が苦手な人」でも理解できるように分かりやすくご紹介します。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

還元算① 逆算のやり方

還元算をするためには逆算を理解している必要があります。

逆算とは計算の関係を利用して、四則計算(＋，−，×，÷の計算)を逆に計算することです。逆算はわからない数を求めたり、答えの確かめ算を行うときに使用します。

また逆算するときのポイントとして、計算できる部分は先に計算をして、式を簡単にしておくことです。実際に例題を解いて詳しいやり方を説明していきます。

例題1

20＋(150-□)÷5＝22 この式の□に当てはまる数を求めなさい。

解説

まずは□に数があるものとして計算の順序を考えて、その順序と逆に計算をしていきます。順序は下のようになります。

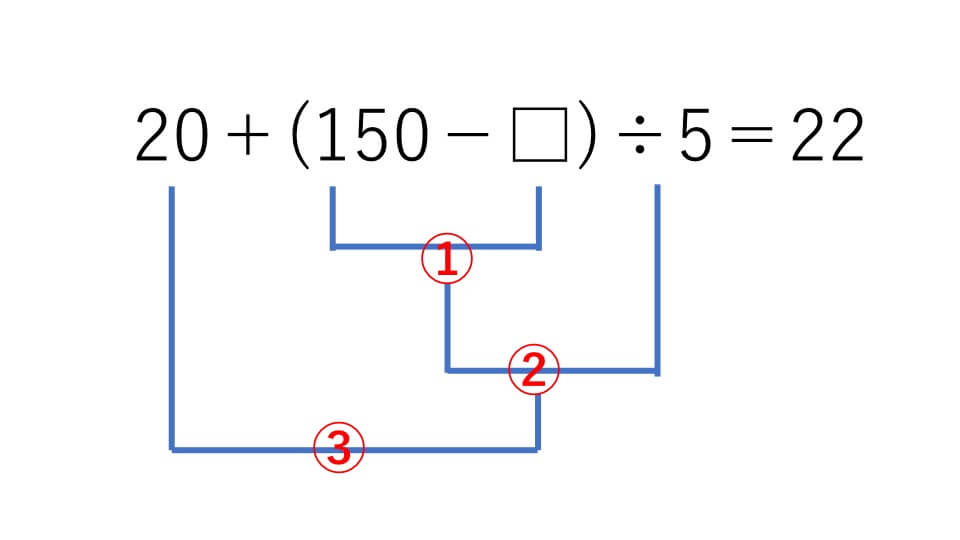
③から計算をします。式をできるだけ小さくしていきたいので、両辺から20を引きます。そうすると左辺から20は消えて、右辺は20が引かれます。

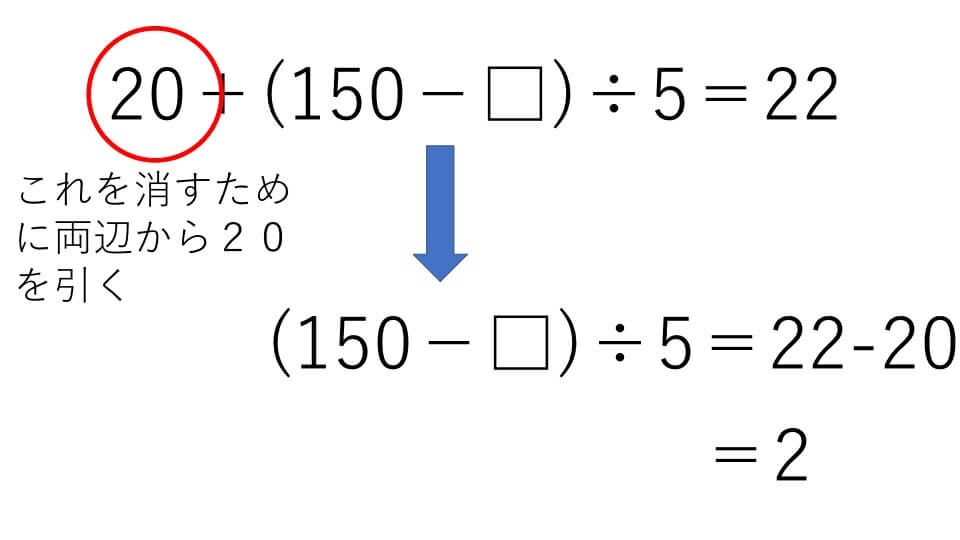
上の式のようになります。次は左辺にある÷5が邪魔なので、÷5を消すために両辺に×5をします。すると左辺から÷5は消えて、右辺には×5が残ります。

すると残りは150−□＝10となるので

答え□＝140

例題2

20−□×(2＋3)÷5＝15 この式の□に当てはまる数を求めなさい。

解説

まずは計算できる部分があれば計算をして式を出来るだけ簡単にしておきます。

これ以上計算できるものはないので、次は式を出来るだけ小さくしていきます。そうすると

□×1＝20-15と式を変形することができます。

ですので

□×1＝5となり

答え5

ここまでの逆算のポイントをまとめると

この4つのポイントを押さえることで逆算をすることができます。

還元算② 還元算のやり方

還元算とはわからない数量を含む問題を逆算を利用して解くことを言います。

還元算の流れは、わからない数量を□として、問題文に沿って式を立てます。そして逆算を利用して□を求めます。

また、間違えて計算をした後、正しい計算の答えを求める問題が出題された場合は、間違えて計算した式をつくって、ある数を求めてから、正しく計算して答えを求めます。

例題3

ある数を5倍した数から6を引いて、次に2で割ると、2になりました。このときのある数を求めなさい。

解説

ある数を□として考えて、問題文に沿って計算の式を作ると

(□×5-6)÷2＝2となります。

この式を逆算すると以下の通りになります。

よって、答え□＝2

例題4

20からある数を引いた差を3倍し、その積から6引いた数を3で割ると、13になりました。このときのある数を求めなさい。

解説

ある数を□として考えて、問題文のとおりに計算の式を作ると

｛(20−□)×3-6｝÷3＝13

この式を逆算すると以下のようになります。

よって答え□＝5

例題5

ある数から2を引いて5倍するのを間違えて、5倍してから2を引いたので23になりました。このときの正しい答えを求めなさい。

解説

間違えた計算を□を使った式で表し、まずは□を求めます。そして、正しい計算の式を作って、正しい答えを求めていきます。

ある数を□として考えて、間違えた計算の式を立てると、

□×5−2＝23となります。この式を逆算すると以下のようになります。

よって□＝5となります。

そしてこの数字を使って正しく計算をすると

(5−2)×5＝15

答え15

還元算③ 入試問題にチャレンジ

入試問題1(明治学院中)

ある数に、その4/13を加え、その和から31を引くと、20になります。ある数はいくつですか。

解説

ある数を□として考えて、問題文のとおりに計算の式を作ると

□×(1＋4/13)−31＝20  

ここで「□×(1＋4/13)」の部分が理解できない人が多いと思います。なぜこのような式になるのかというと、問題文の「ある数に、その4/13を加え」という文に注目してください。ある数に4/13を加えたのではなく、その数の4/13を加えたことが分かると思います。ですので「□×(1＋4/13)」という式になります。

計算できる部分は計算をしてなるべく簡単な式に直すので

□×17/13−31＝20となります。

この式を逆算すると以下のようになります。

よって答え□＝39

入試問題2(相模女子大中)

ある数に1/3を加えてから6/5をかけるのを、間違えて1/3をかけて6/5を加えたので、その答えは41/30になりました。正しい答えを求めなさい。

解説

間違えた計算を□を使った式で表し、まずは□を求めます。そして、正しい計算の式を作って、正しい答えを求めていきます。

ある数を□として考えて、間違えた計算の式を立てると、

□×1/3＋6/5＝41/30

この式を逆算すると以下のようになります。

よって□は1/2だと分かります。この数字を使って正しい計算をすると

(1/2＋1/3)×6/5＝1

答え1

まとめ

いかがだったでしょうか？還元算は計算よりも□を使って式を立てるのが難しかったと思います。スムーズに式を立てれるようになるためには、問題数をこなして還元算の問題に慣れていくしかありません。

今回学習した内容を十分に理解してお手持ちの問題集で問題を解いていってください。
次は、つるかめ算のポイント解説です。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】