中学受験の算数で出題される単元「回転体」。教科書やノートは平面上でとてもイメージがしにくい単元です。回転体の問題はどのような立体図形になるのかイメージできればそこまで難しい問題はありません。
今回は、回転体の書き方を詳しく説明していきたいと思います。と立体図形について正しく理解していれば回転体の問題を簡単に解くことができます。
順番としては、立体図形を学んだあとに、回転体を学ぶ必要があります。もしも、立体図形がまだ不安であったり、理解がちゃんとできていない中学受験生はこちらの記事を先に読んだほうが理解が深まります。
この記事は、
- 算数の回転体が苦手な受験生
- 回転体を初めて学習する受験生
が対象です。この記事を読むことで、回転体とはどんなものなのかを正しく理解することができます。
回転体① 回転体とは何?
下の図形を見てください。平面図形を、同じ平面にある1つの直線の周りに1回転させてできる立体図形のことを回転体と言います。
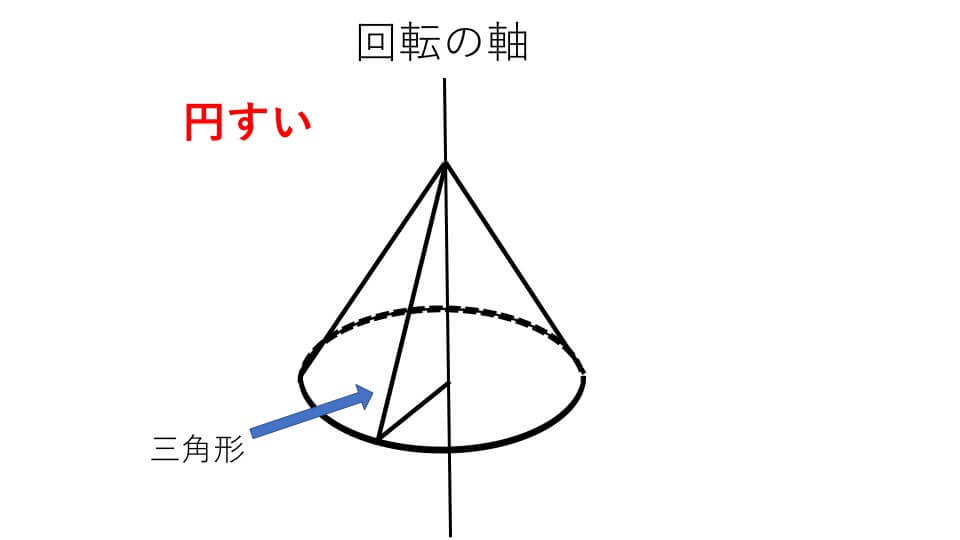
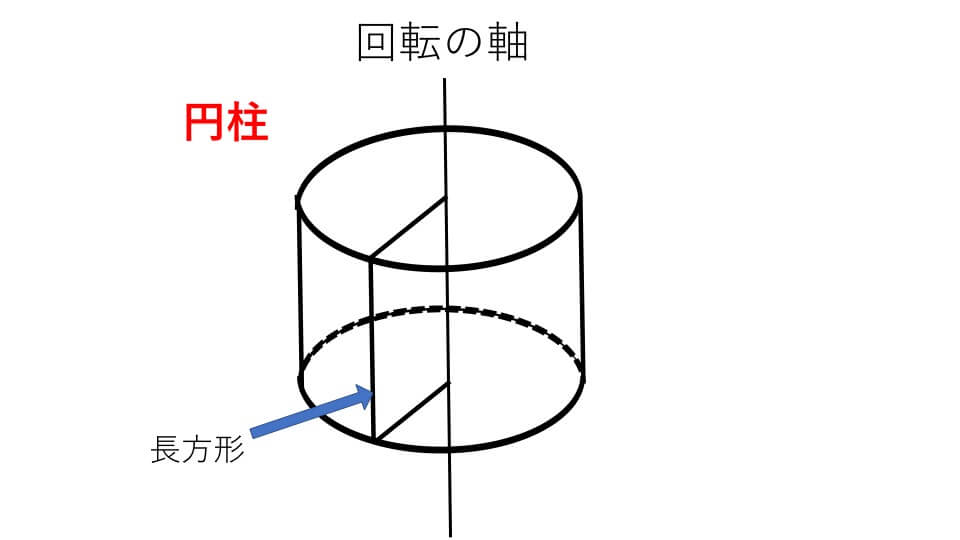
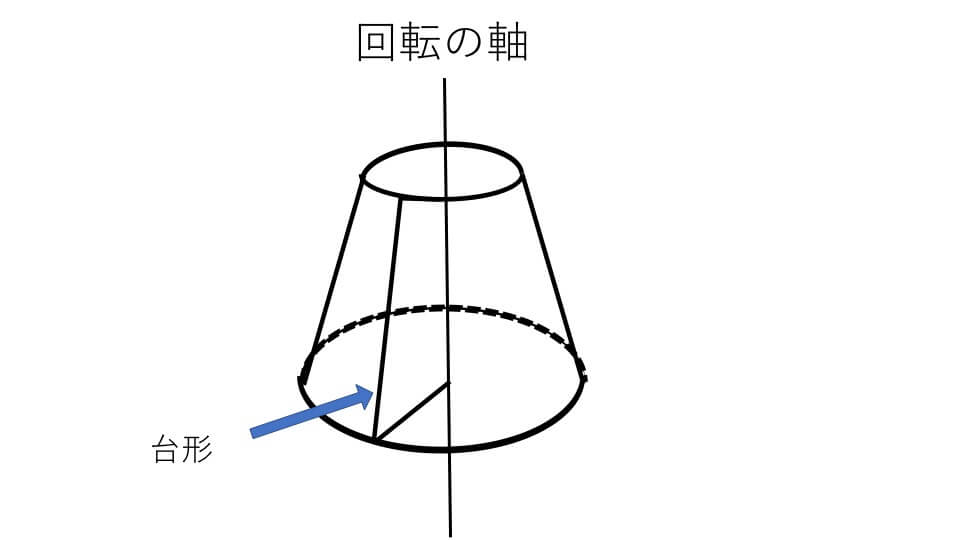
そして図形を一回転させる中心となる軸のことを回転の軸と言います。
ここでポイントです。回転体を、回転の軸に垂直な平面で切ると、必ず切り口は円状になります。なぜなら回転体は図形を円上に回転してできた立体図形だからです。
回転体② 回転体の書き方
例題1
下の図形を直線Aを回転の軸として1回転してできる立体図形を書きなさい。
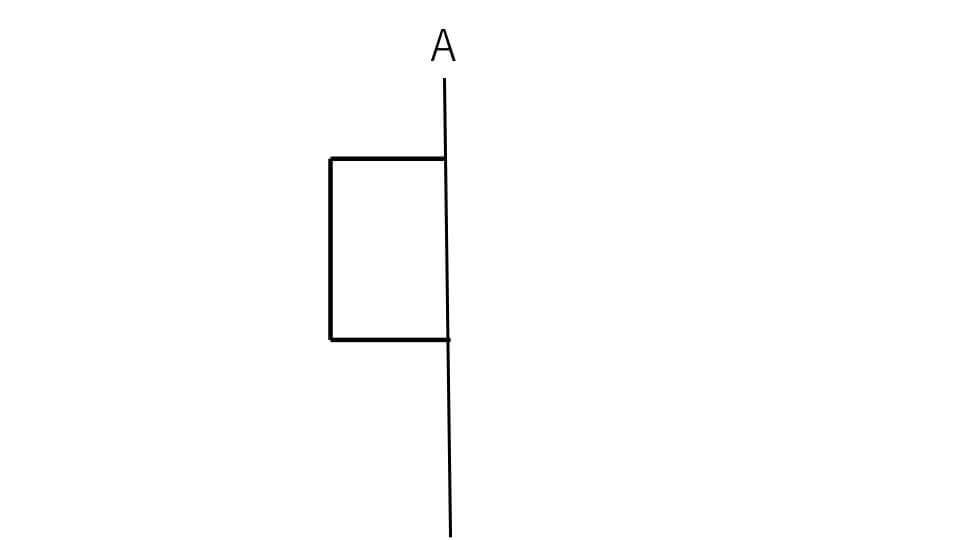
解説
まずは下の図のように左の図形を軸Aの線対称移動させます。
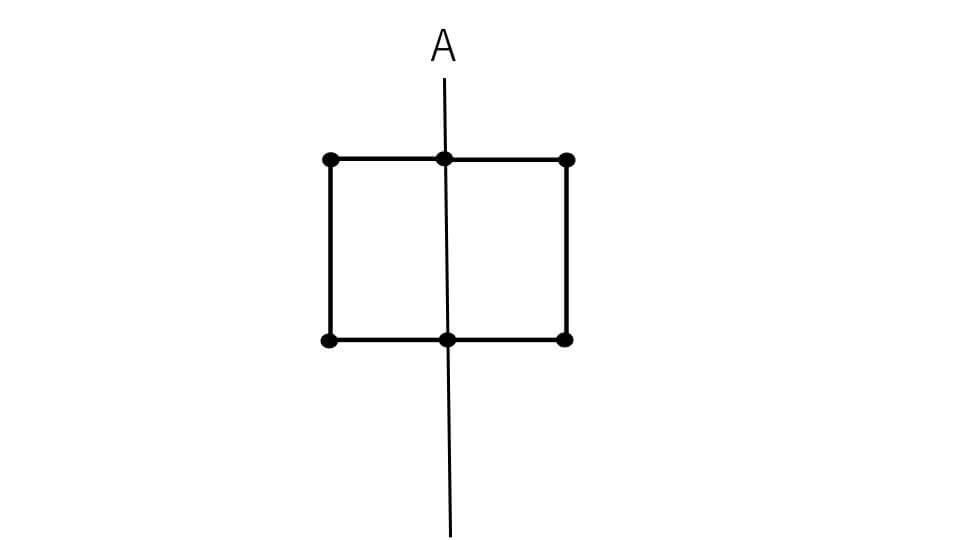
ここでのポイントは角の点を対象に移動させることで、左の図形を移動させると考えてください。ですので、角に点を書いて移動させるとわかりやすいです。
そして対応する点で円を書くと回転体が出来上がります。
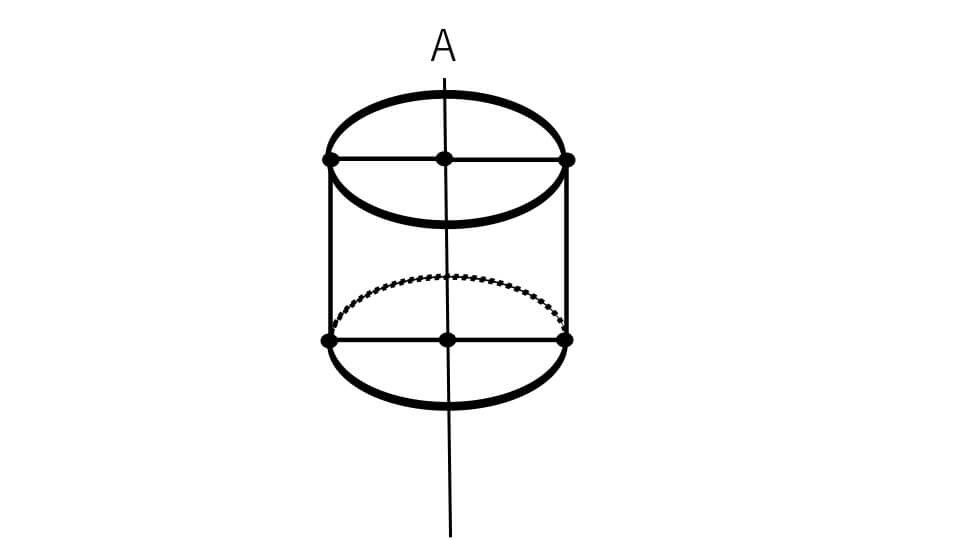
円柱に見えますよね。点線で書かれている部分は自分から見たときは見えない部分のことを表しています。
ここまでの話をまとめると
- 左側の図形を回転軸に対称移動させる。
- 対称移動させるために、図形の角に点をつける。
- 対応する点で円を書く。
この3ステップを忘れないでください。この3ステップを理解して、回転体の立体図形が書けるようになれば、回転体の問題はもう怖くありません。
例題2
下の図形を直線Aを回転の軸として1回転してできる立体図形を書きなさい。
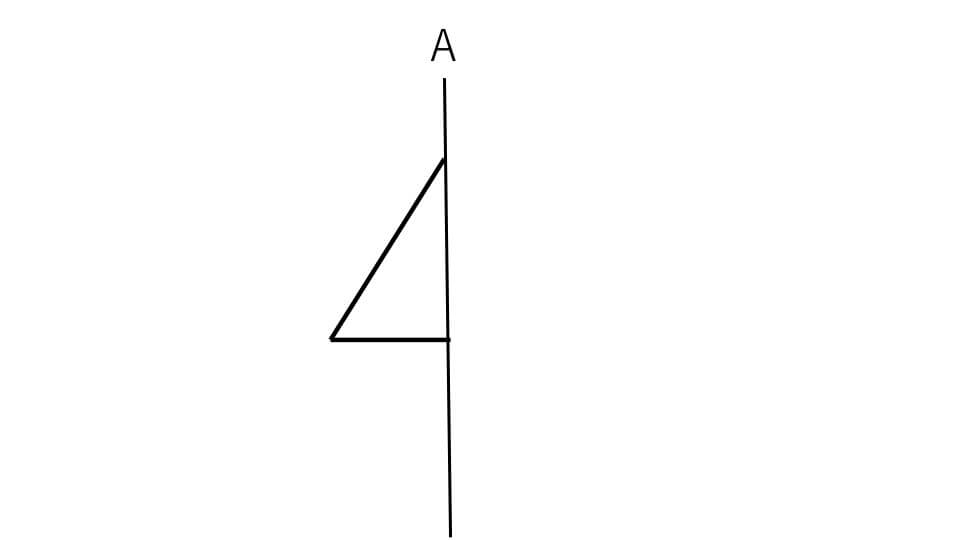
解説
まずは下の図のように角に点をつけて、左側の図形を対称移動させます。
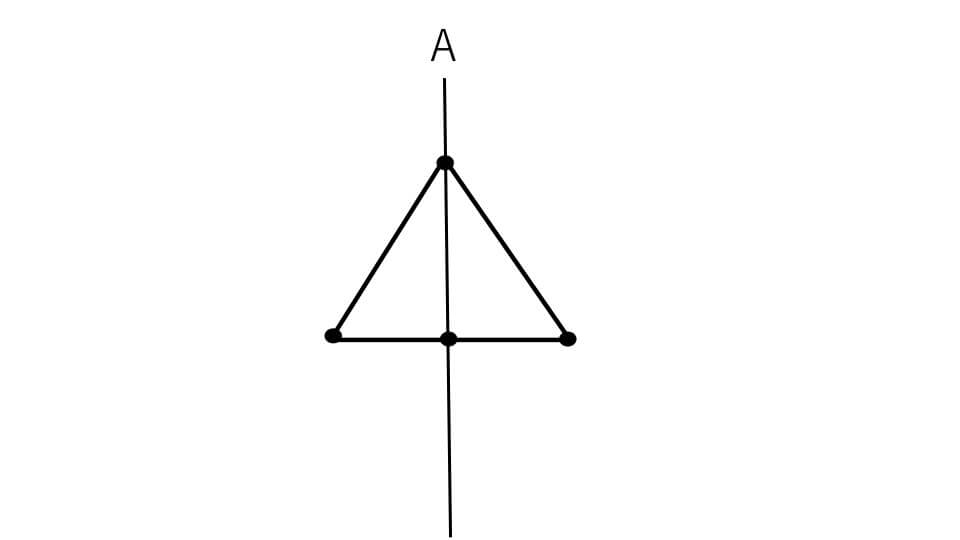
そして対応する点で円を書きます。
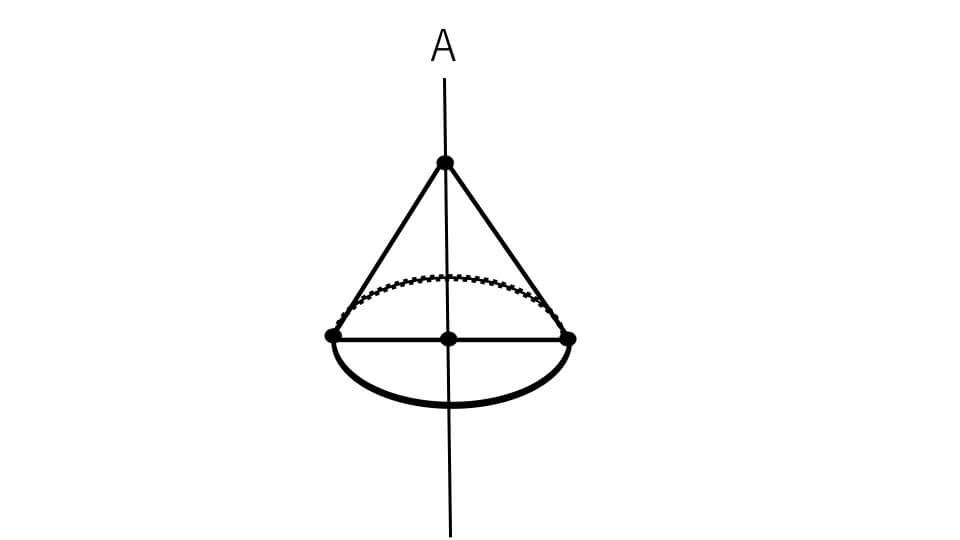
今回は対応する点が2点しかなかったので、円はひとつだけでした。円すいの形になりました。
例題3
下の図形を直線Aを回転の軸として1回転してできる立体図形を書きなさい。
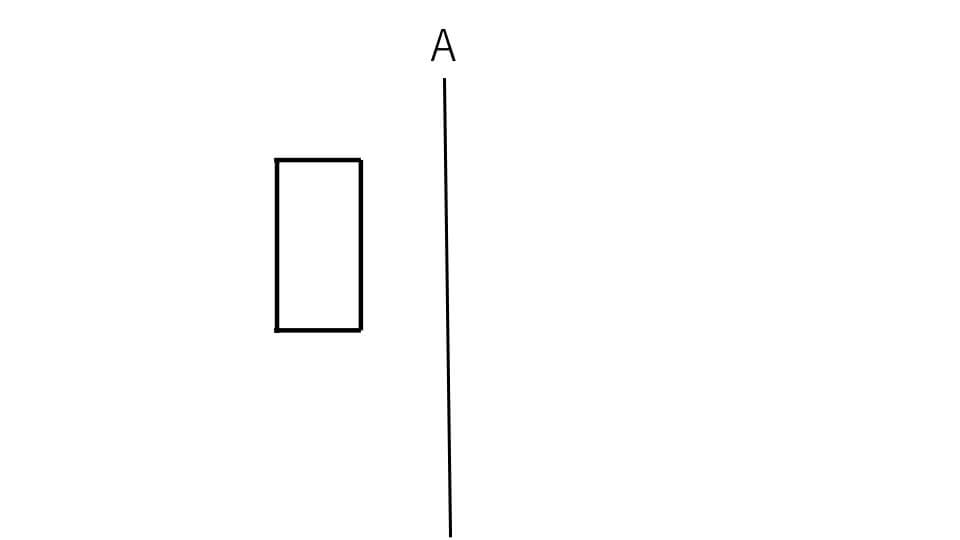
解説
今回の問題は少し変わっています。図形が回転軸から離れています。しかし離れていてもやることは変わりません。まずは下の図のように角に点をつけて、左側の図形を対称移動させます。
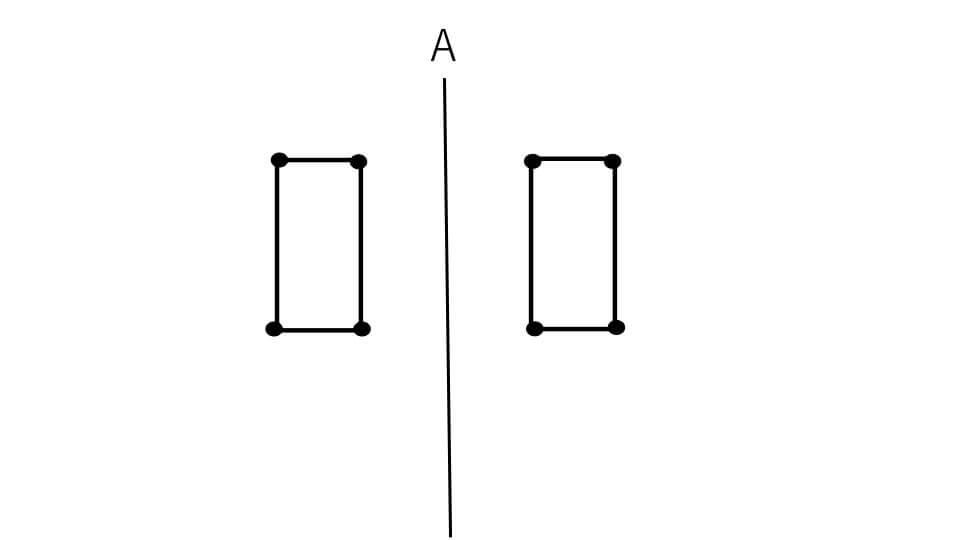
そして対応する点で円を書きます。
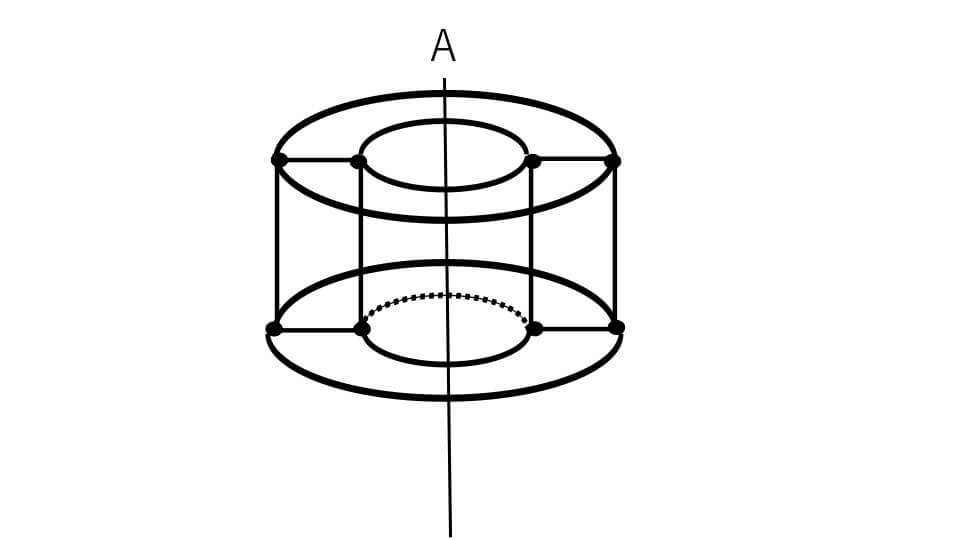
今回は点がいくつもあったので全て円を書きました。この立体図形の真ん中に空どうができているイメージが付きますか?
このようにして不規則な形がきても回転体を書く3ステップを理解することでどんな回転体でもイメージすることができます。あとは出てきた問題の回転体を書いて問題文にそって問題を解いていくだけです。
回転体③ 回転体の体積の求め方
例題4
下の図を見てください。回転軸Aで次の三角形が1回転したときにできる立体図形の体積を求めなさい。円周率は3.14とします。
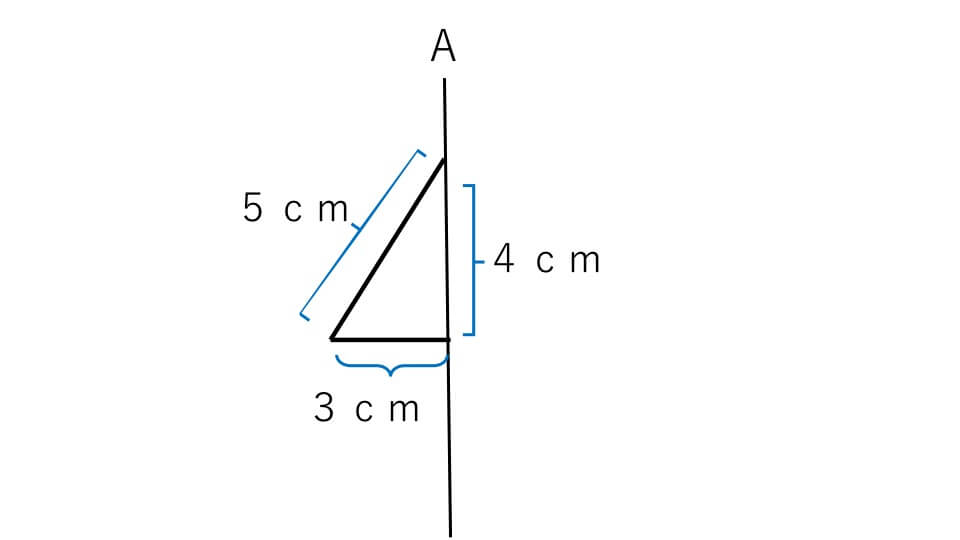
解説
回転体を書いて問題を解いていきます。まずは下の図のように角に点をつけて、左側の図形を対称移動させます。
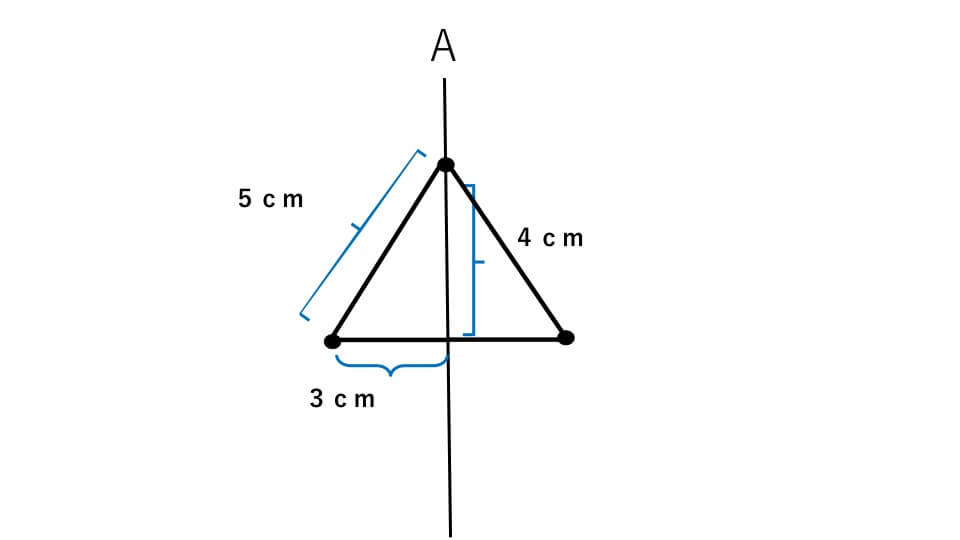
そして対応する点で円を書きます。
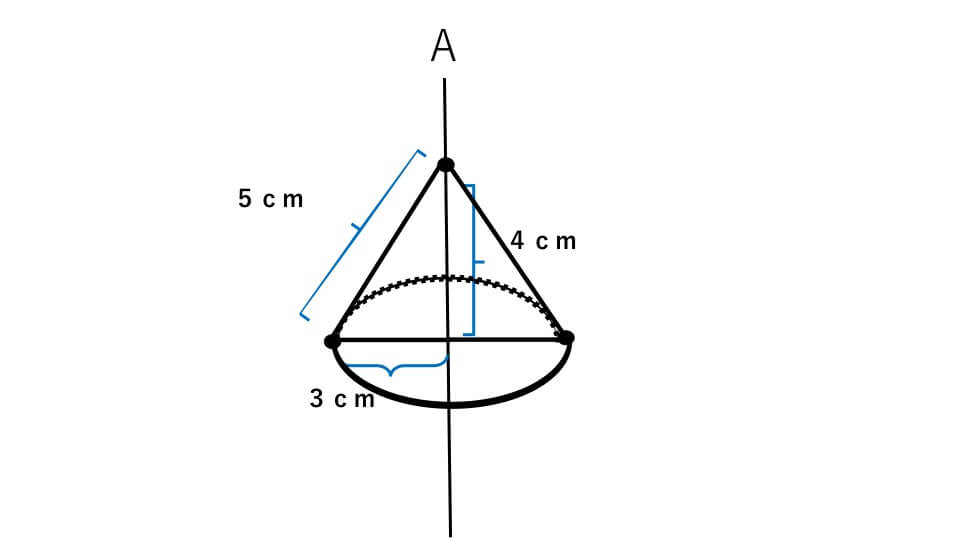
そうすると底面の半径が3cmで高さが4cmの円すいになりました。円すいは「半径×半径×3.14×高さ÷3」で求めることができるので、3×3×3.14×4÷3=37.68㎤となります。
例題5
下の図を見てください。回転軸Aで次の三角形が1回転したときにできる立体図形の体積を求めなさい。円周率は3.14とします。
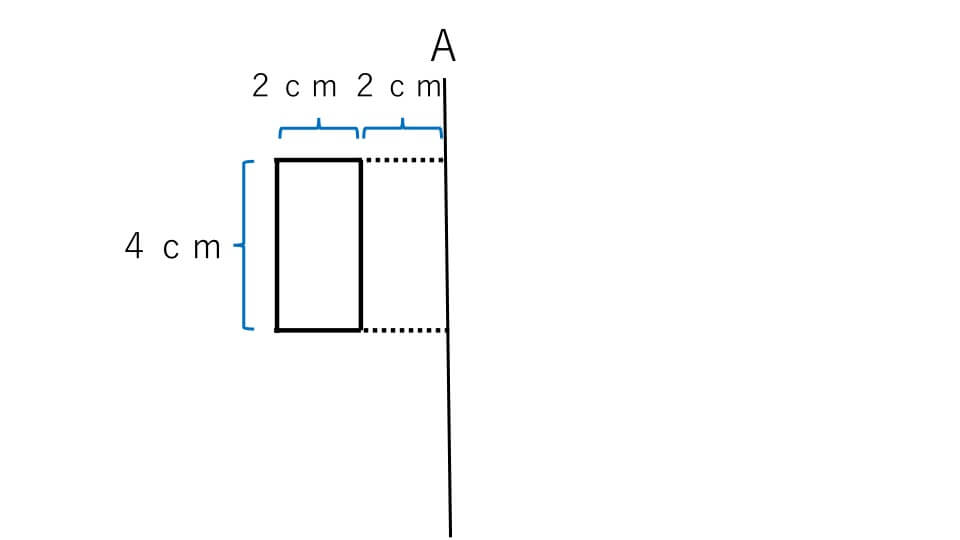
解説
回転体を書いて問題を解いていきます。まずは下の図のように角に点をつけて、左側の図形を対称移動させます。
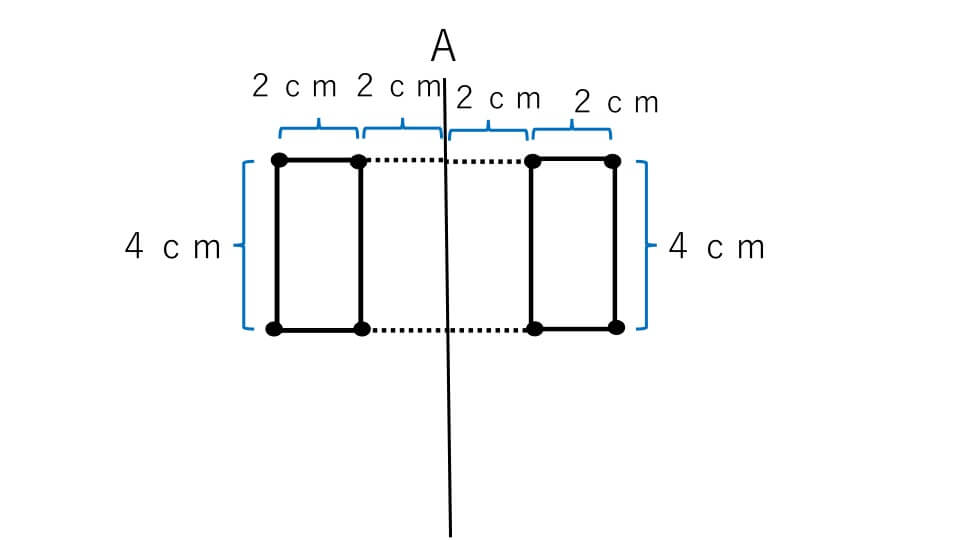
そして対応する点で円を書きます。
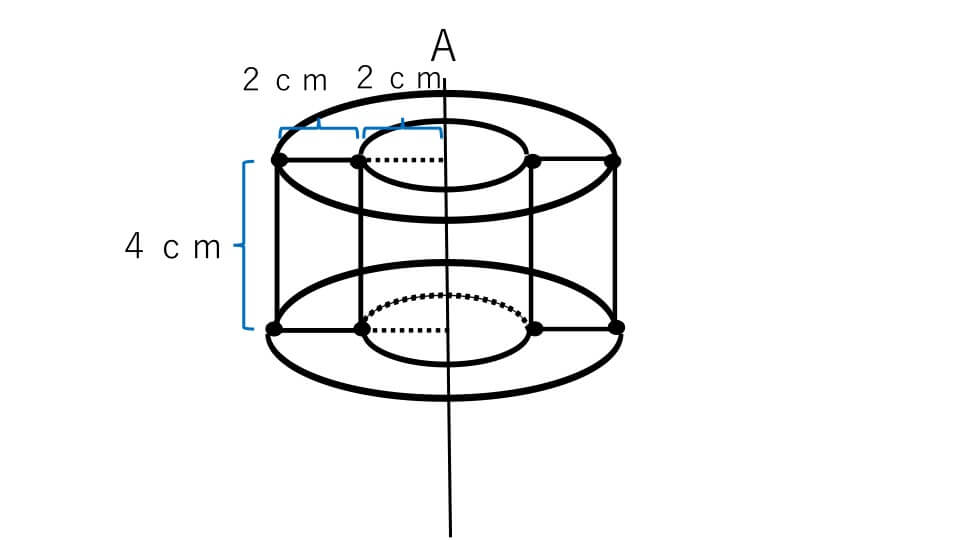
上の図のような中の円柱をくり抜いた円柱になります。大きい円柱の体積から小さい円柱の体積を引けば、この立体図形の円柱の体積を求めることができます。円柱の体積の求め方は「底面積×高さ」なので、
小さい円柱の体積=2×2×3.14×4=50.24㎤
大きい円柱の体積=4×4×3.14×4=200.96㎤
よって200.96−50.24=150.72㎤
まとめ
いかがだったでしょうか?
回転体の問題は自力で回転体を書くことができればどんな問題がきても解けるということがわかってもらえたと思います。今回お伝えした「3ステップの書き方」をマスターして回転体の問題を解いてください。
最後までご覧いただきありがとうございました。

