中学受験 算数 平面図形の面積 ~成り立ちから詳しく解説~

中学受験の算数で出題される重要単元「平面図形」。角度や辺、面積を求めたり、比で表したりします。この単元では、図形の性質と基本公式をしっかり覚えておくことがポイントです。

覚えておきたい面積の求め方は、四角形(正方形・長方形）、平行四辺形、台形、ひし形、三角形の5つとなっています。

しかし面積を覚える時に、どうしてその式が成り立つのか理解している子どもはほとんどいません。大人でもちゃんと説明できる人はほとんどいなのではないでしょうか？公式の成り立ちを理解することで、公式を忘れることはまずありませんし、平面図形の問題に対する考え方の柔軟性が身に付きます。

今回の記事では平面図形の面積の求め方を成り立ちから詳しく解説していきます。

• 算数の平面図形の分野が苦手な人
• 公式をなかなか覚えられない人

そんな人たちでもこの記事を読むことで、理屈から理解でき、平面図形の問題が得意になります。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

平面図形① 四角形の面積公式の成り立ち

そもそも面積とは何かというと広さのことを言います。算数によく出題される面積の単位は㎠(平方センチメートル)です。1辺が1cmの正方形の面積が1㎠です。

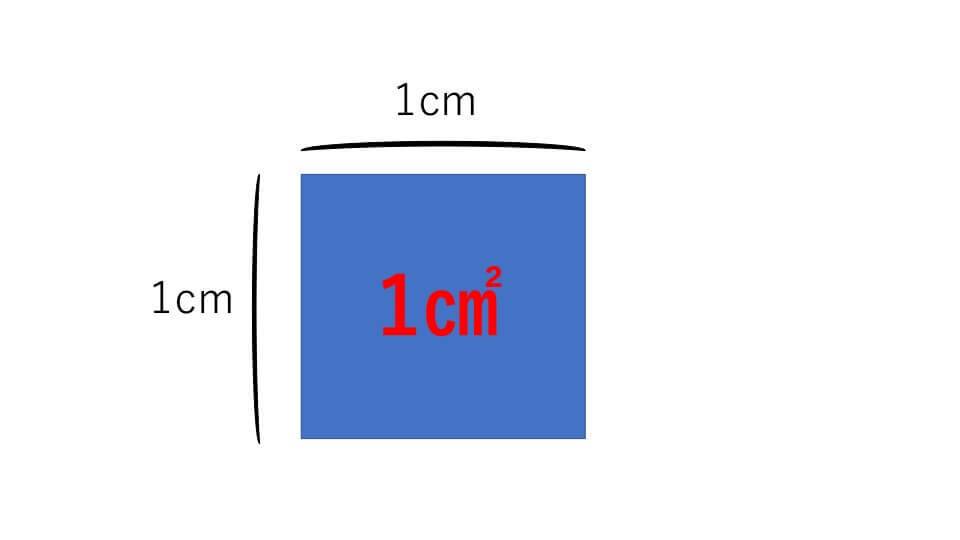
これから説明していくにあたり、重要な部分なので、しっかりと覚えてください。

具体例を用いて説明していきます。

例題1

次の長方形の面積を求めなさい

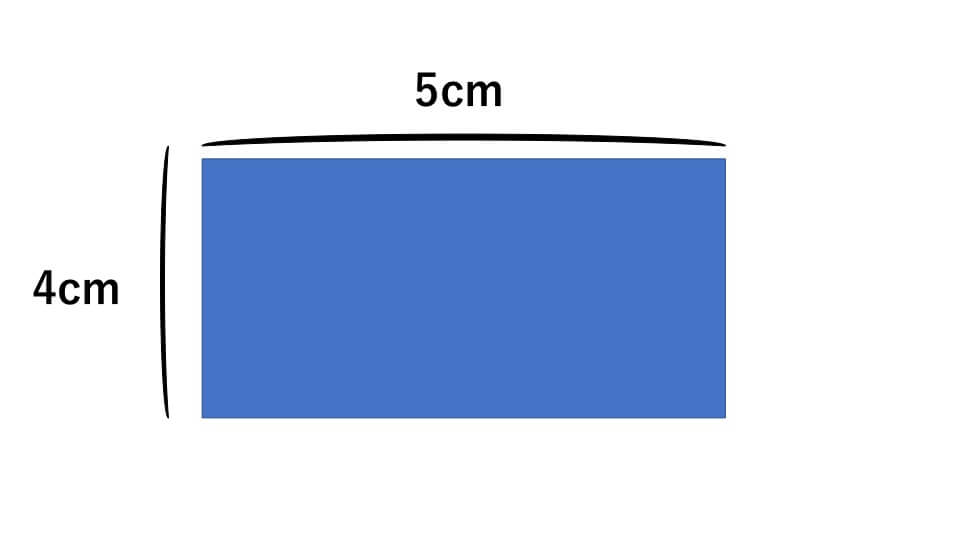
解説

この長方形の面積はたて×よこ＝4×5＝20㎠となります。ではなぜ、長方形の面積は「たて×よこ」で求めることができるのでしょうか？

すでに「1辺が1cmの正方形の面積が1㎠」であることは述べました。ですので、「(例題1)の長方形の中に1辺が1cmの正方形が何個あるのか」を求めれば、長方形の面積が求めることができます。

(例題1)の長方形のたてとよこを1cmずつに刻むと下の図のようになります。

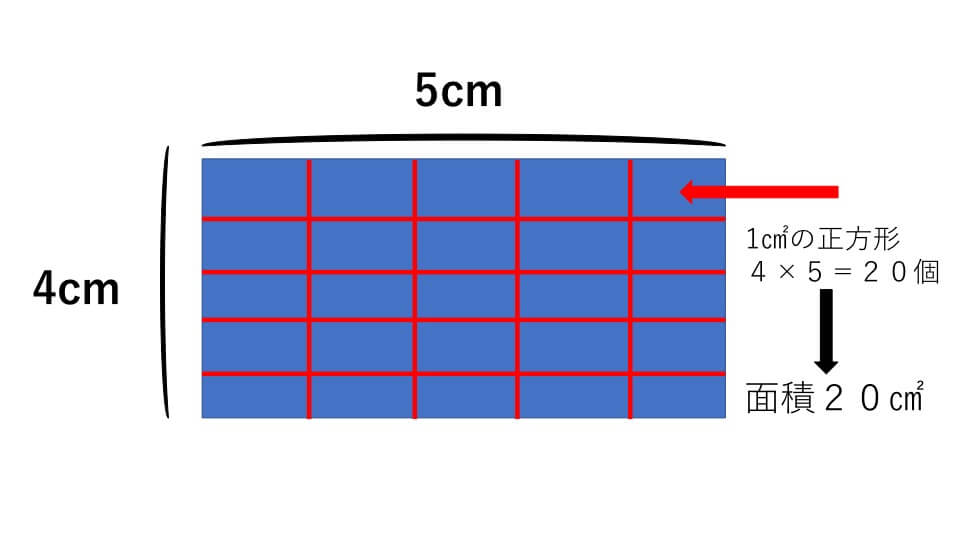
長方形のたてには4個の正方形が並び、よこには5個の正方形が並んでいます。つまり長方形の中に、正方形が3×4＝12 個並んだということになります。ですので、1㎠の正方形が12 個並んだので、(例題1)の長方形の面積は12 ㎠となります。

(例題1)の長方形のたてとよこに並ぶ正方形の数(4個と5個)とたてとよこの長さ(4cmと5cm)は同じです。ですので長方形の面積は「たて×よこ」で求めることができるのです。

具体例を用いて説明していきます。

例題2

次の正方形の面積を求めなさい。

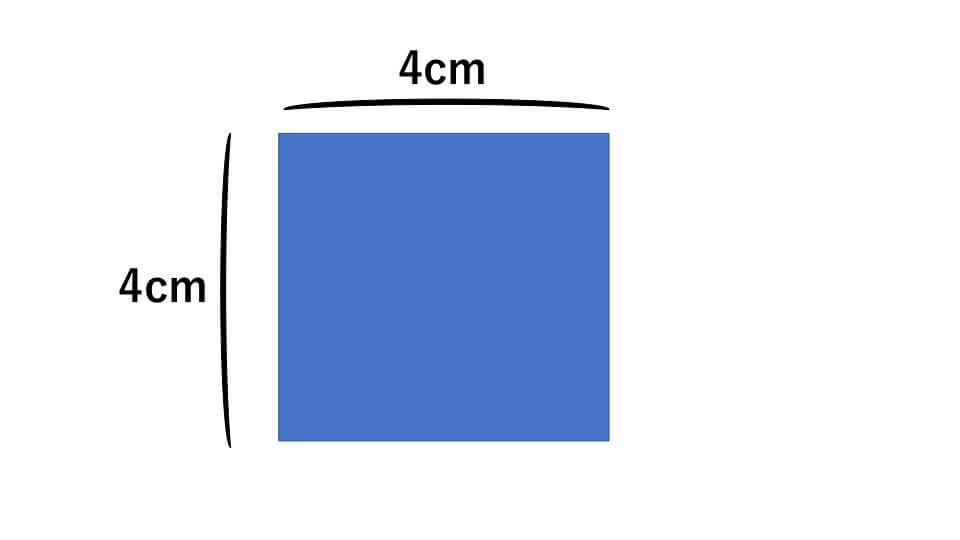
解説

この正方形の面積は「1辺×1辺＝4×4＝16㎠」と求めることができます。しかしどうして正方形の面積は「1辺×1辺」で求めることができるのでしょうか？

その理由は長方形と同様の説明が成り立ちます。(例題2)の正方形の1辺1cmずつ刻むと下の図のようになります。

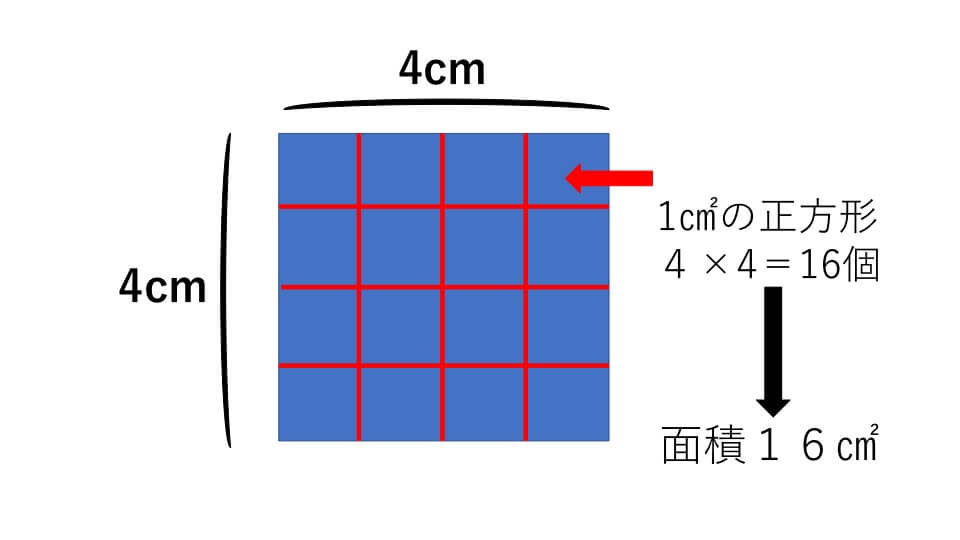
(例題2)の正方形に1辺が1cmの正方形(1㎠)が4×4＝16個並んだということがわかります。1㎠の正方形が16個あるので(例題2)の正方形の面積は16㎠と求めることができます。

(例題2)の正方形の1辺に並ぶ小さい正方形の数(4個)と1辺の長さの数(4cm)は同じです。ですので、正方形の面積は「1辺×1辺」で求めることができるのです。

平面図形② 平行四辺形の面積公式の成り立ち

平行四辺形とは2組の向かい合う辺がそれぞれ平行な四角形のことを言います。

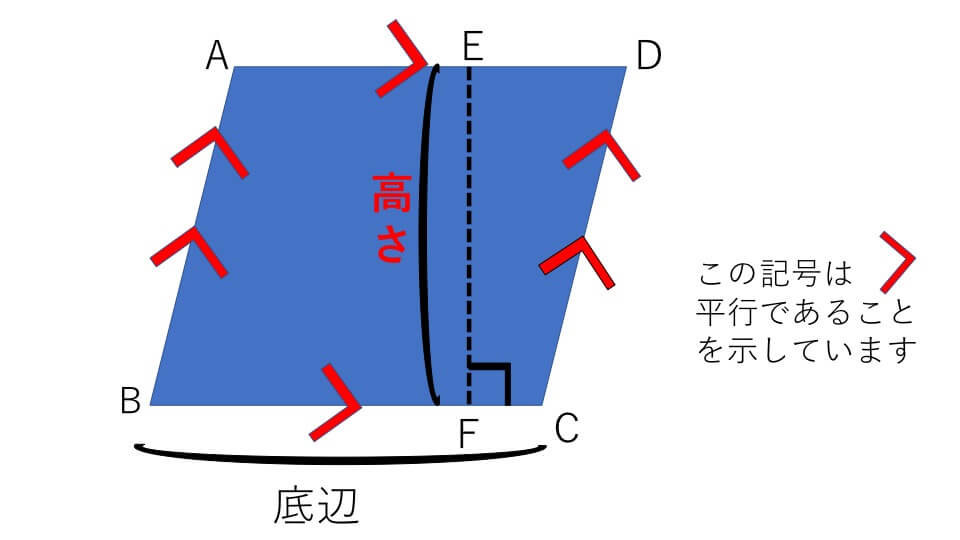
上の図の平行四辺形で辺BCを底辺としたとき、その辺に垂直な直線EFの長さを高さといいます。

具体例を用いて成り立ちについて説明します。

例題3

次の平行四辺形の面積を求めなさい

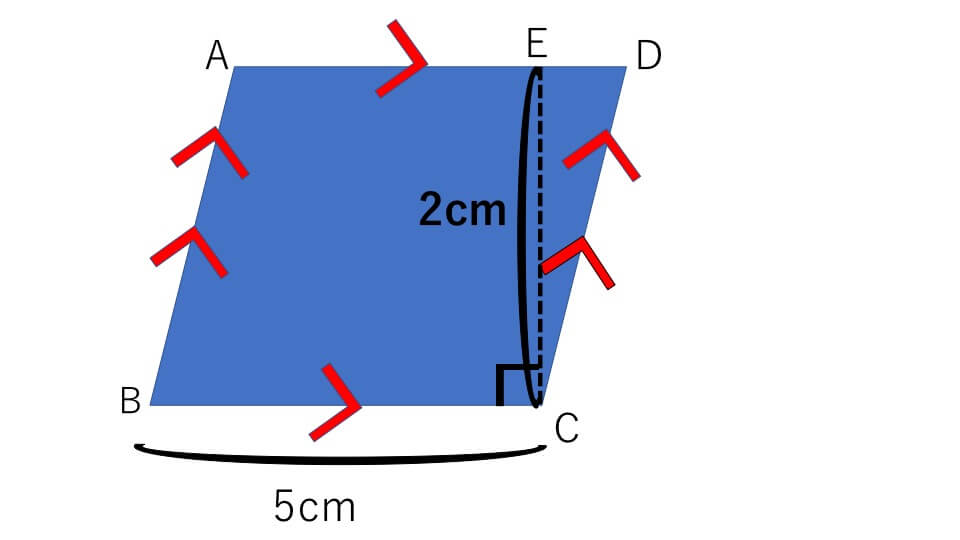
解説

この平行四辺形の面積は「底辺×高さ＝5×2＝10㎠」と求めることができます。しかしどうして平行四辺形の面積は「底辺×高さ」で求めることができるのでしょうか。

(例題3)の平行四辺形で三角形CDEを下の図のように左のほうに移動させます。すると平行四辺形ABCDが長方形FBCEに変形します。

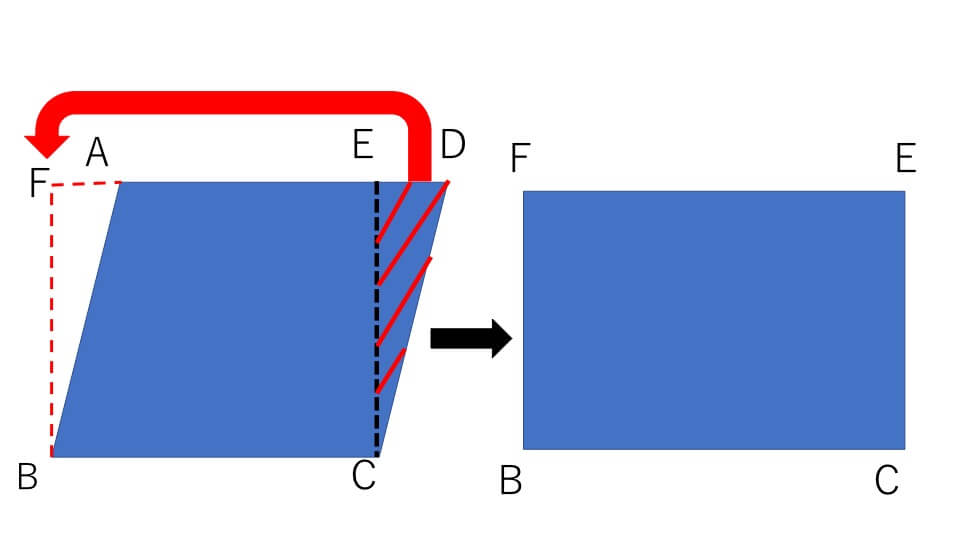
長方形FBCEの面積は、底辺BCの長さ(よこ5cm)と高さCEの長さ(たて2cm)をかけて、5×2＝10㎠と求めることができます。ですので、長方形FBCEの面積、つまり平行四辺形ABCDの面積は「底辺×高さ」で求めることができるのです。

平面図形③ 台形の面積公式の成り立ち

台形は1組の向かい合う辺が平行な四角形のことです。

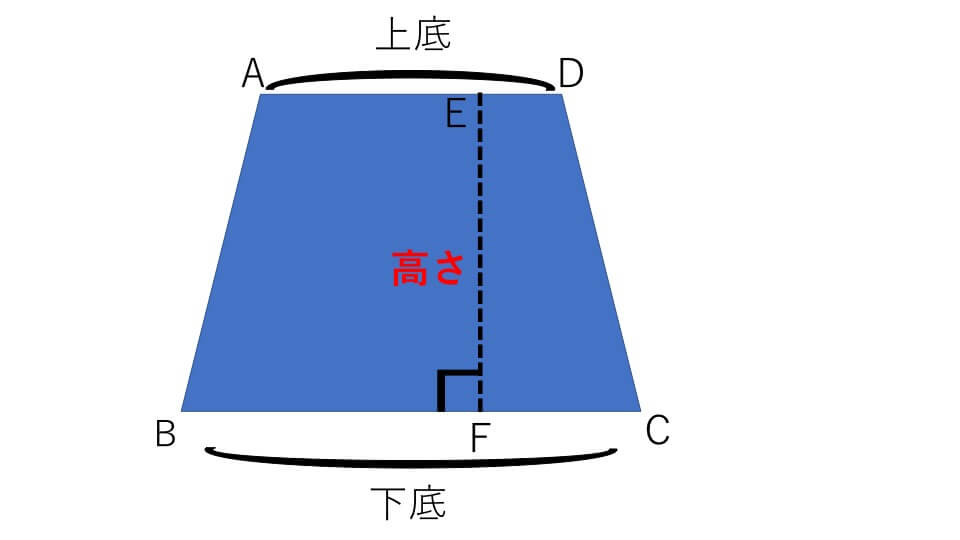
上の台形で平行な辺AD、辺BCを上底、下底と言います。そして上底と下底に垂直な直線EFの長さを高さと言います。

具体的な例を用いて成り立ちについて説明します。

例題4

次の台形の面積を求めなさい。

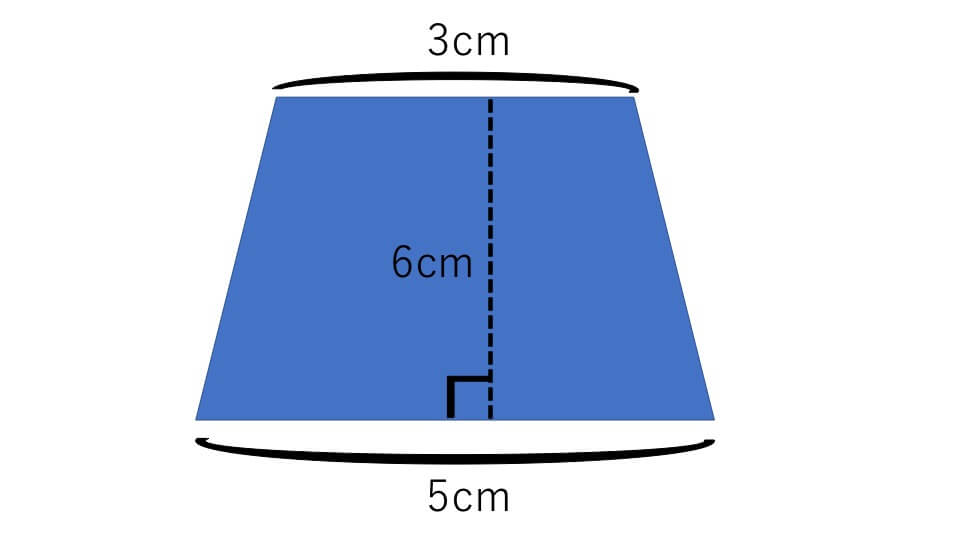
解説

台形の面積は「(上底＋下底)×高さ÷2＝(3＋5)×6÷2＝24㎠」と求めることができます。しかし、どうして台形の面積は「(上底＋下底)×高さ÷2」で求めることができるのでしょうか。

(例題4)の台形と同じ台形を、上下逆さまにしてくっつけると、下の図のような平行四辺形になります。

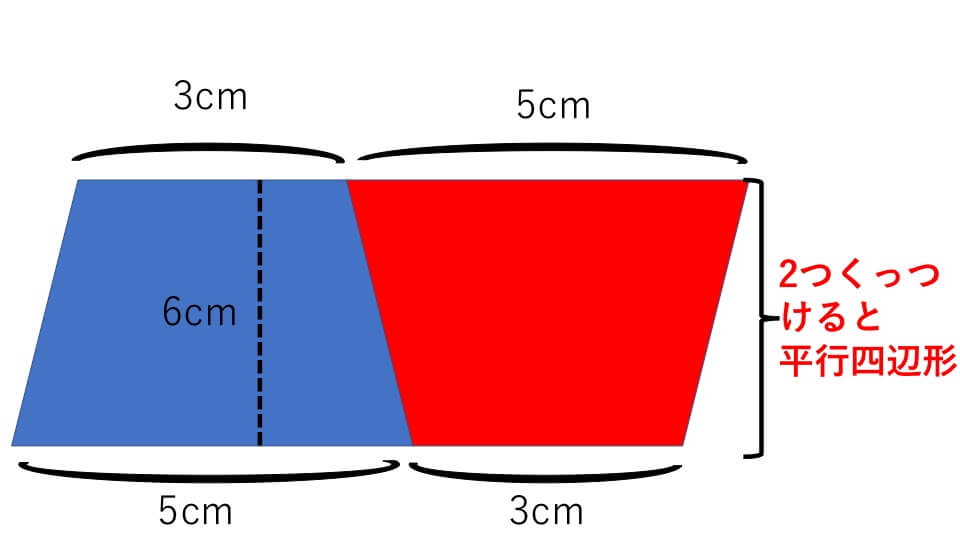
この平行四辺形に底辺は、もとの台形の上底と下底をたした長さになるので、この平行四辺形の面積は「(上底＋下底)×高さ」で求めることができます。しかしもとの台形の面積は、平行四辺形の半分ですので、「(上底＋下底)×高さ÷2」で求めることができます。これにより、(例題4)の台形の面積は(3＋5)×6÷2＝24㎠であることがわかります。

平面図形④ ひし形の面積公式の成り立ち

ひし型とは4本の辺の長さが等しい四角形のことを言います。また四角形などで、となり合わない2つの頂点を結ぶ直線のことを対角線と言います。

具体的な例を用いて成り立ちについて説明します。

例題5

次のひし型の面積を求めなさい

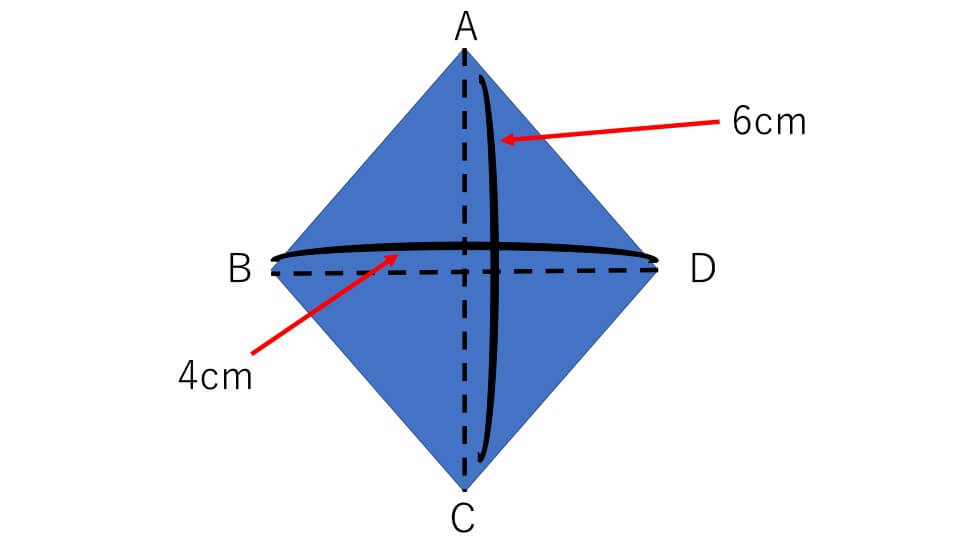
解説

このひし型の面積は「対角線×対角線÷2＝6×4÷2＝12 ㎠」と求めることができます。しかしどうしてひし形の面積は「対角線×対角線÷2」で求めることができるのでしょうか。

ひし型には「2本の対角線が直角に交わる」性質があります。(例題5)のひし型は2本の対角線ACとBDによって、下の図のように4つの同じ直角三角形に分けることができます。

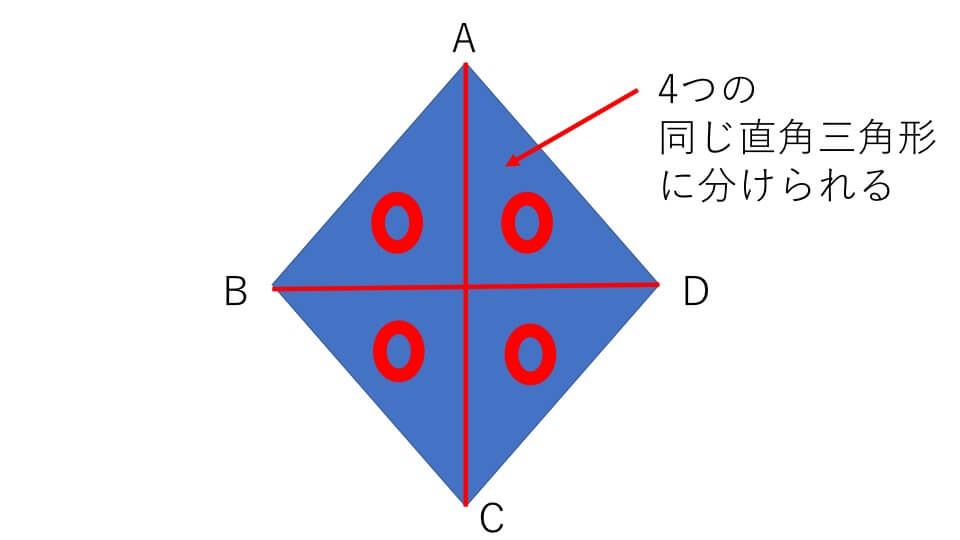
そして、このひし型の外側に、さらに4つの同じ直角三角形をくっつけると、下の図のように、長方形EFGHを作ることができます。

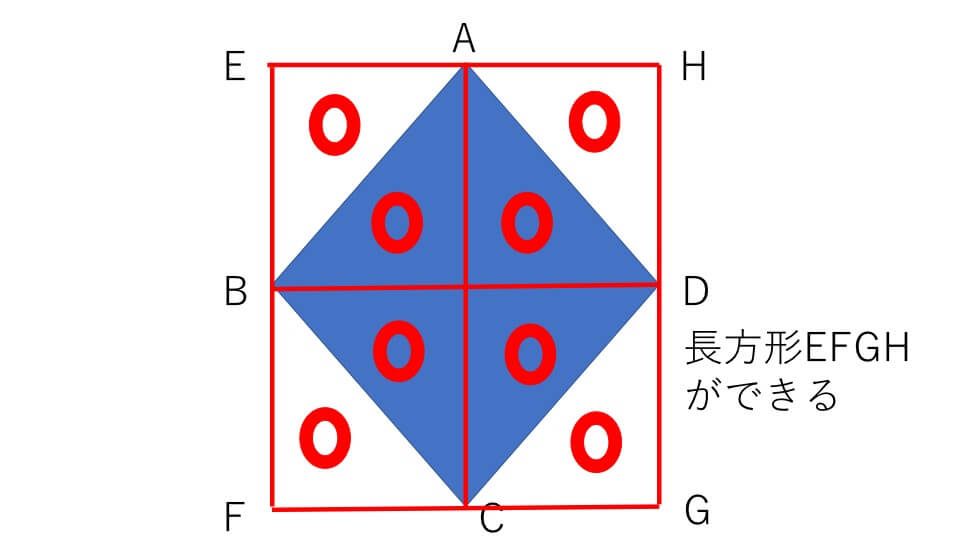
長方形EFGH(直角三角形8個分)の面積は「(ひし形)の対角線×対角線」で求めることができます。一方で、ひし形(直角三角形4個分)の面積は長方形EFGHの半分ですので、「対角線×対角線÷2」で求めることができます。つまり(例題5)にひし形の面積は6×4÷2＝12 ㎠となります。

平面図形⑤ 三角形の面積公式の成り立ち

具体的な例を用いて成り立ちについて説明します。

例題6

次の三角形の面積を求めなさい。

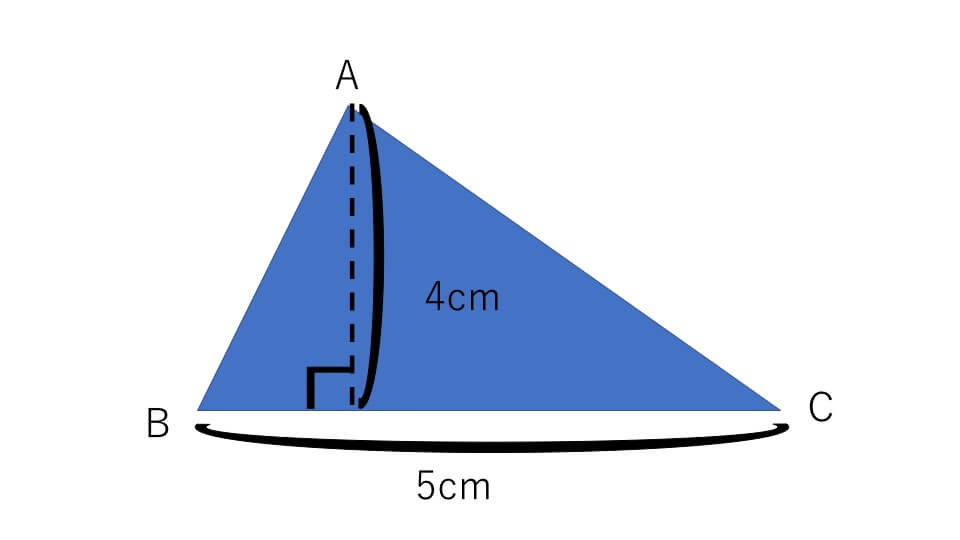
解説

三角形ABCの面積は「底辺×高さ÷2＝5×4÷2＝10㎠」と求めることができます。しかしどうして三角形の面積は「底辺×高さ÷2」で求めることができるのでしょうか。

下の図のように(例題6)の三角形ABCと同じ三角形ACDをくっつけると平行四辺形ABCDになります。

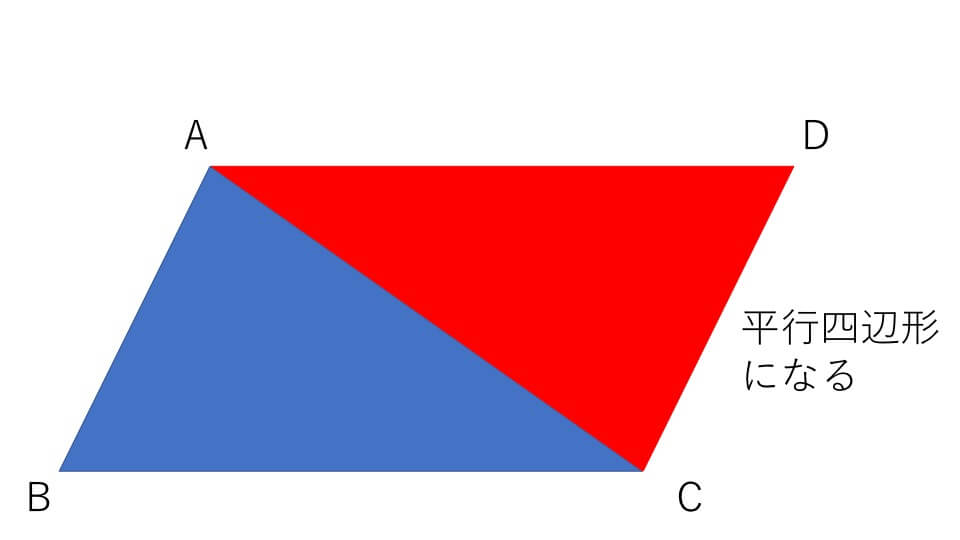
平行四辺形の面積は「底辺×高さ」で求めることができるので、平行四辺形ABCDの面積は5×4＝20㎠です。しかし求めたい三角形ABCは平行四辺形ABCDの半分なので、5×4÷2＝10㎠と求めることができます。ですので、三角形に面積は「底辺×高さ÷2」で求められるのです。

まとめ

長方形、正方形、平行四辺形、台形、ひし形、三角形の5つの平面図形に関して、面積公式が成り立つ理由について解説してきました。算数の平面図形の問題ではこれらの図形が組み合わさってできています。

ですので今回の成り立ちを理解することで、どんな応用問題でも対応することができます。公式が成り立つ理由を知った上で、より深く算数を理解し、根本から考える力を養っていきましょう。

次は展開図のポイント解説です。平面図形を理解したうえで展開図に進むことでより理解が深まります。

いかがだったでしょうか？回転体の問題は自力で回転体を書くことができればどんな問題がきても解けるということがわかってもらえたと思います。今回お伝えした「3ステップの書き方」をマスターして回転体の問題を解いてください。

最後までご覧いただきありがとうございました。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】