中学受験 算数 場合の数 ~例題を使ってポイント解説~

中学受験の算数で出題される単元「場合の数」。ある事柄の起こり方が何通りあるのかを考える単元です。通りを数えるときに見落としてしまったり、重複や数え間違いが出てしまい苦手とする子が多い単元です。中学受験だけでなく、今後の高校受験、大学受験にも大きく関わってくる単元なので、十分な対策を行い、今のうちに基礎を固めておきたい単元です。

この記事では、算数が苦手な人や、場合の数を初めて学習する人、すでに塾で一度習ったが苦手な人でも理解しやすいように、わかりやすく解説しています。この記事を読むことで、場合の数とは何か本質的に理解でき、どのような問題にも対応できるようになります。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

場合の数① 基本事項

場合の数の問題を解く上で必ずマスターしてほしいものがあります。それは樹形図です。樹形図とは、いくつかのものの中から何個か選んで、問題の条件に従って順序よく並べた図のことを言います。

例えば、A、B、Cの並べ方は何通りあるのか求めたいときは、下の図のような樹形図を書きます。

樹形図を書くときによく、思いついた並べ方をただがむしゃらに書く人がいますが、これだと見落としが多くなってしまいます。樹形図を書くときは見落としや重なりがないように、順序よく書くことが大切です。

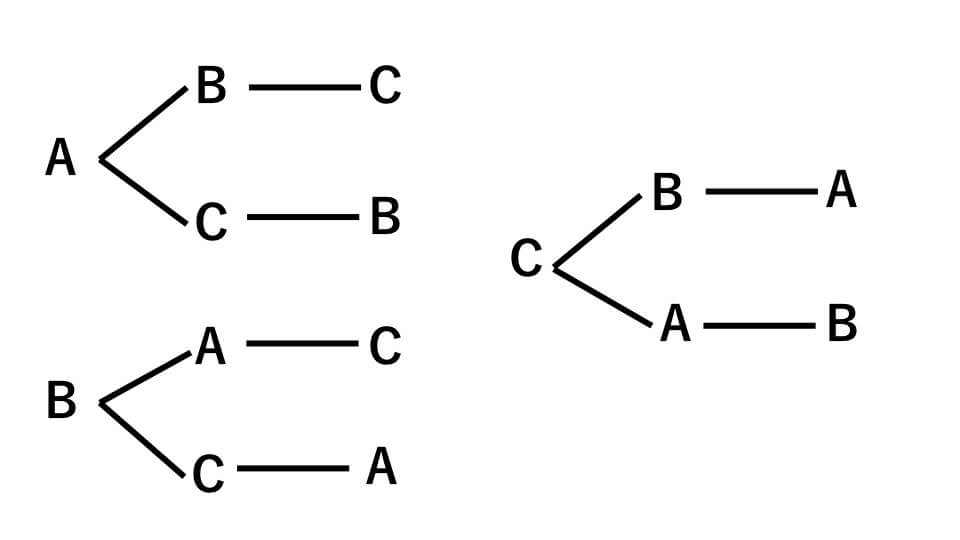
また問題によっては樹形図ではなく表や計算を使って考えた方が解きやすい問題もあります。

場合の数② 並べ方

例題1

A君、B君、C君、D君の4人でソフトボール投げをしました。投げる順番は何通りあるか求めなさい。

解説

これは簡単な問題で、樹形図を書けばすぐにわかります。下の図のような樹形図を書いてください。

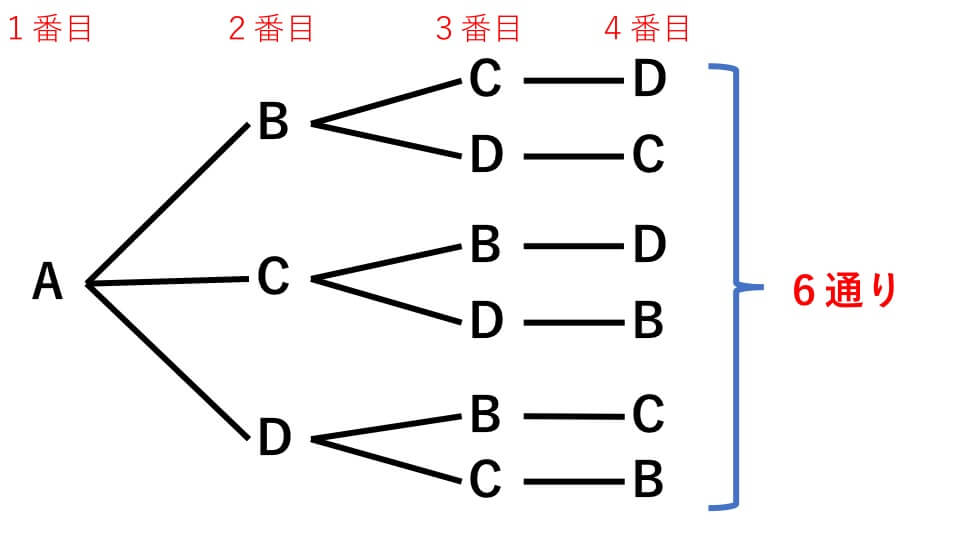
この樹形図は1番目にA君が投げる場合の樹形図です。A君が1番目に投げる場合の順番は6通りあることが分かると思います。

B君、C君、D君が1番目のときがそれぞれあり、同じように樹形図を書くことができます。ですので、4人が投げる順番は全部で、

6×4＝24

よって、答え　24通り

別解

樹形図を書かず、計算のみで解きたい場合は以下のように考えます。

• 1番目に投げる人はA君、B君、C君、D君の4通り
• 2番目に投げる人は1番目に投げる人を除く3通り
• 3番目に投げる人は1、2番目に投げる人を除く2通り
• 4番目に投げる人は、1、2、3番目に投げる人を除く1通り

ですので、全部で、

4×3×2×1＝24

よって、答え　24通り

例題2

A君、B君、C君、D君、E君の5人が1列に並びます。次の場合の並び方は何通りあるか求めなさい。

(1)A君が真ん中にくる並び方

(2) B君とC君が隣り合う並び方

解説

(1)から解説します。

下の図のようにA君の場所は最初から決まっているので、求めるのはA君以外の4人の並び方です。

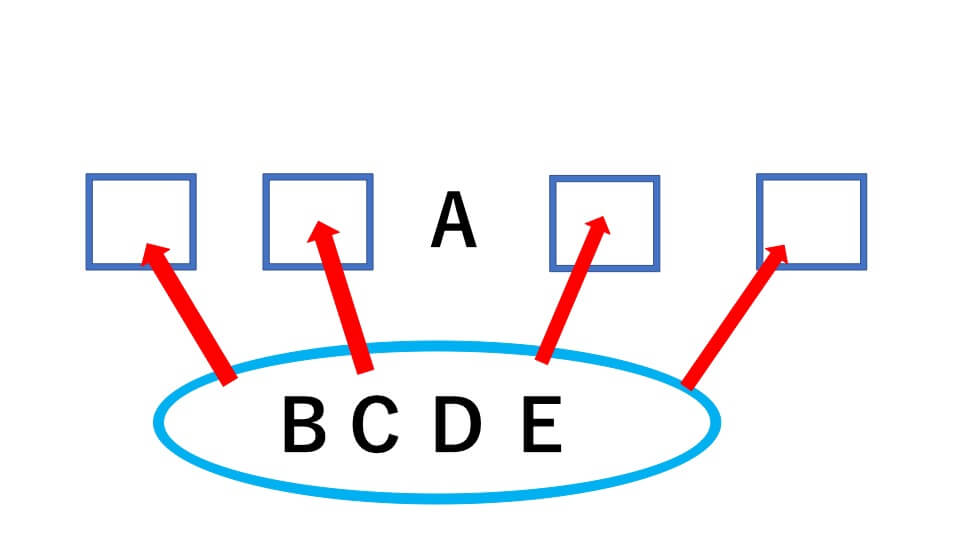
ですので、並び方は、

4×3×2×1＝24

よって、答え　24通り

＊計算を使って考えるのが苦手な人はB君、C君、D君、E君の4人の並び方を求めるときに樹形図を書いて考えてもいいです。

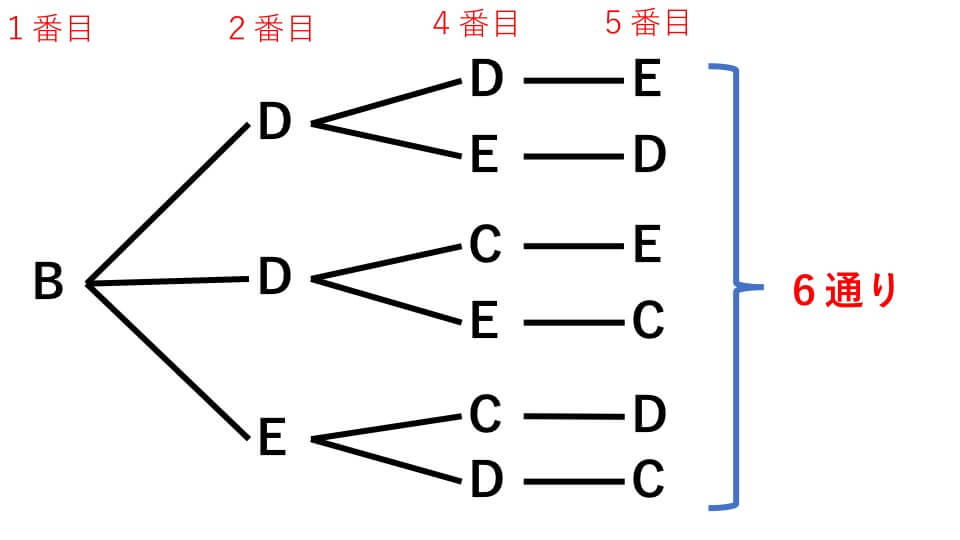
上の樹形図のようにB君を1番目にしたとき6通りあることがわかります。C君、D君、E君が1番目の場合も同じ形の樹形図ができるので、全部で、

6×4＝24通り

(2)の解説をします。

隣り合う合うということは「B君C君」または「C君B君」の順番があることがわかります。ですので、B君とC君をまとめて1人として考えます。すると下の図のようになります。

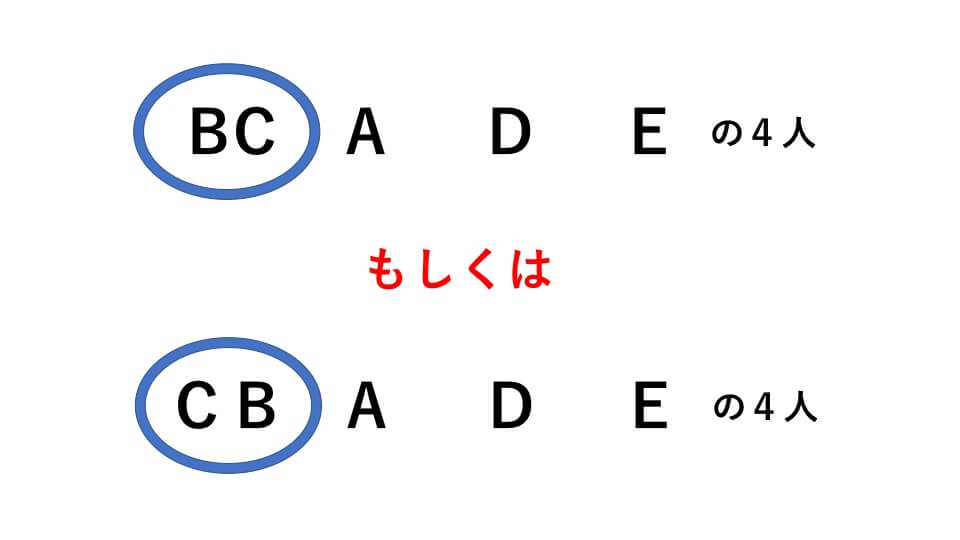
求める並び方は「BC、A、D、Eの4人」「CB 、A、D、Eの4人」と考えることができるので、全ての並び方はこの2通りの並び方の和になります。ですので式は、

(4×3×2×1)+ (4×3×2×1)＝48

よって、答え　48通り

例題３

大小の2つのサイコロを同時に投げます。次の場合何通りあるのか求めなさい。

(1)出る目の数のは和が6以上になる場合

(2)出る目の数の積が偶数になる場合

解説

(1)から解説していきます。

2つのサイコロが出てくる問題では、必ず表を作って考えてください。

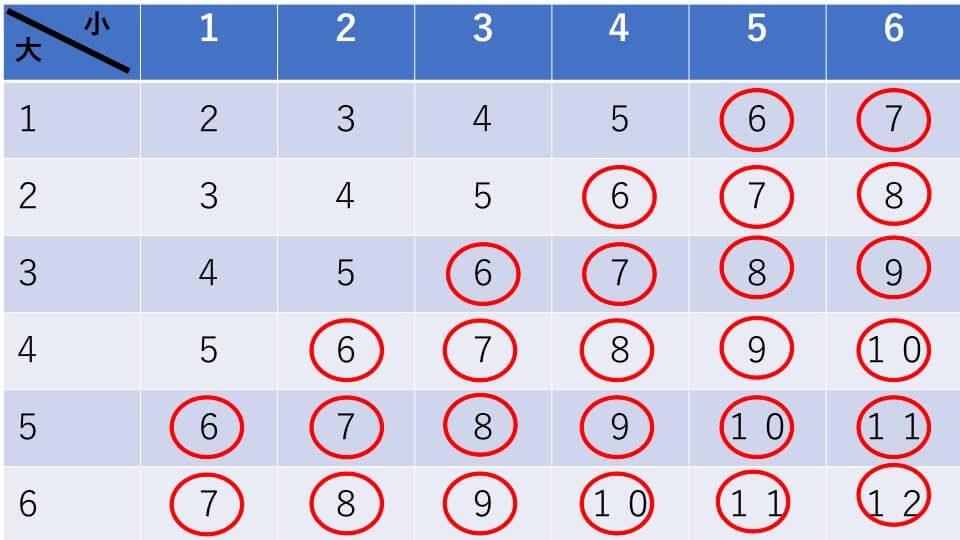
上の表を使って和が6以上になる通りを数えると、答えが分かります。

よって、答え　26通り

(2)の解説をします。

(2)も同じように表を作って考えます。

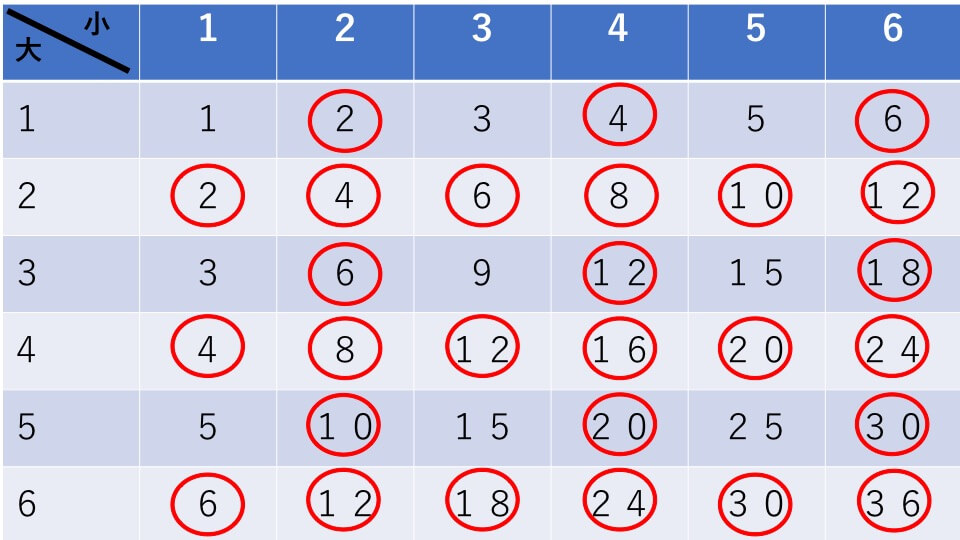
上の表を使って積が偶数になる通りを数えると、答えが分かります。

よって、答え　27通り

中学、高校でも2つのサイコロの問題が出題されますが、表を書くことで必ず正解できる問題となっています。得点源となるので、必ず覚えておきたい問題です。

例題４

下の図のような道があります。このときAからBまで行く道順は何通りあるのか求めなさい。ただし右か上しか進めないものとします。

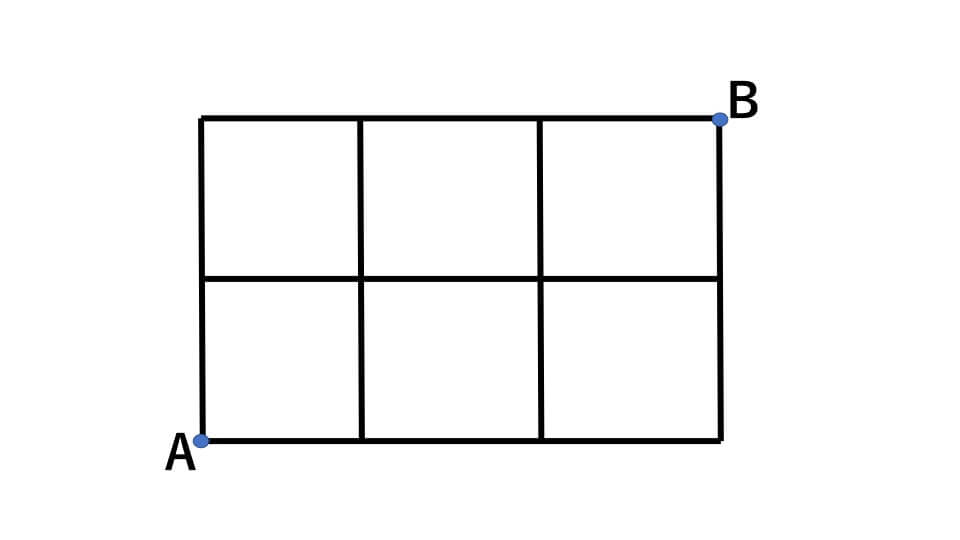
解説

道順を考える問題では道と道が交わる点ごとに道順を表す数を書いて考えていきます。

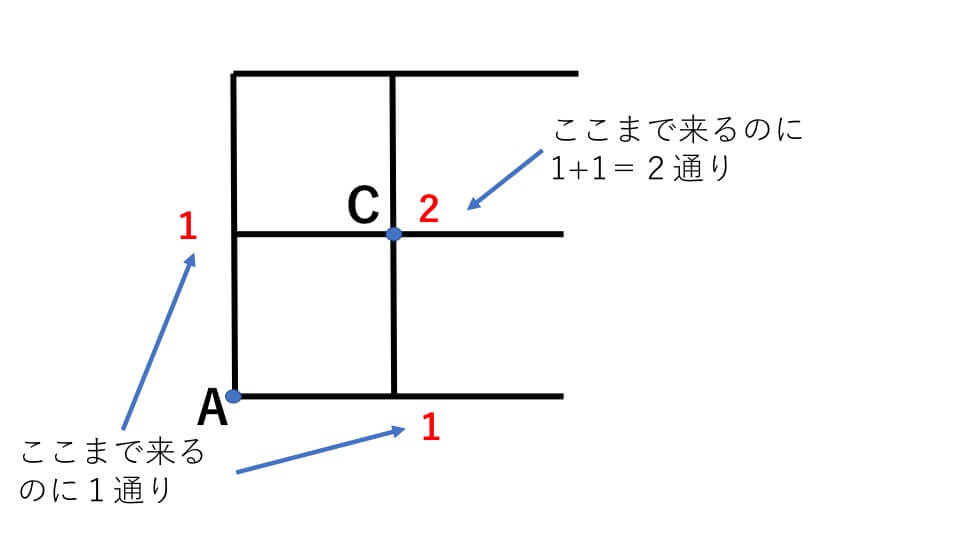
AからCまでの道順は、Cの左の道から来る場合(1通り)、Cの下の道から来る場合(1通り)の合わせて2通りあります。

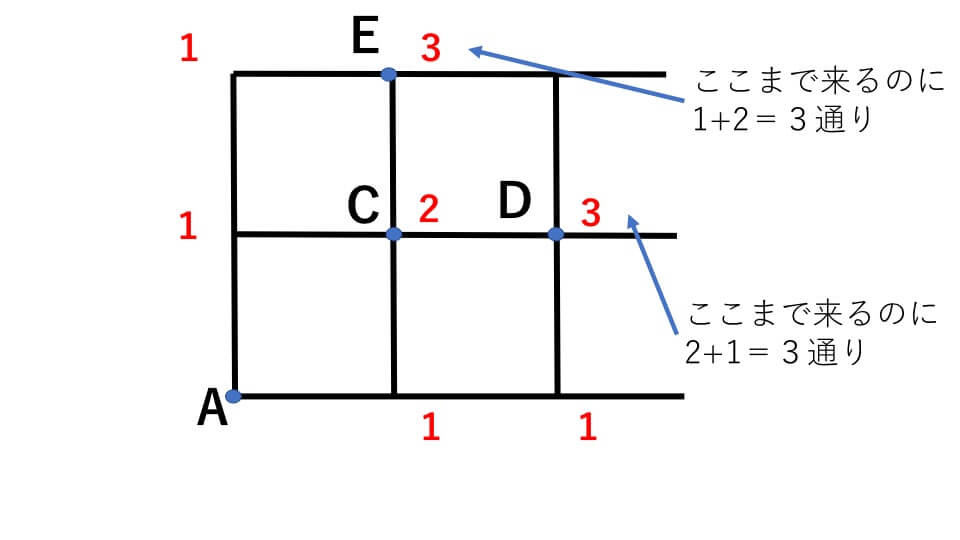
先程と同じようにして考えていきます。AからDまでの道順は、Dの左の道から来る場合(2通り)、Dの下から来る場合(1通り)の合わせて3通りあります。同じようにしてAからEまでの道順も3通りだとわかります。

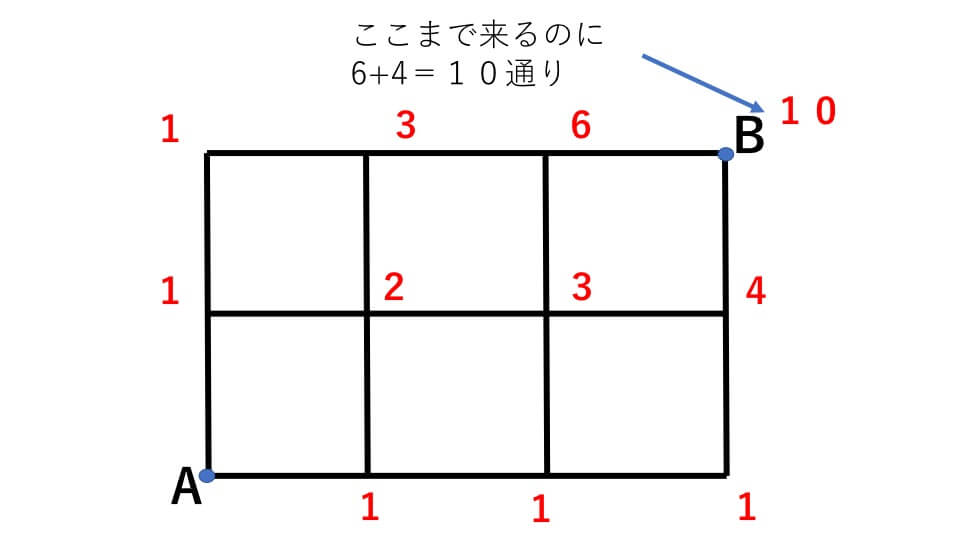
このように全ての道と道が交わる点ごとに道順を左と下の数の和を計算して考えていきます。AからBまでの道順は、Bの左から来る場合(6通り)と下から来る場合(4通り)があるので合わせて、

6+4＝10

よって、答え　10通り

場合の数③ 組み合わせ

例題５

A君、B君、C君、D君、の4人の中から、2人図書委員を選ぶとき、選び方は何通りあるか求めなさい。

解説

今までの問題とは違い、順番は関係ありません。例えばA君とB君の二人を選ぶとき「AB」と「BA」の違いは無いのです。

それを考慮して考えると、下の樹形図のようになります。

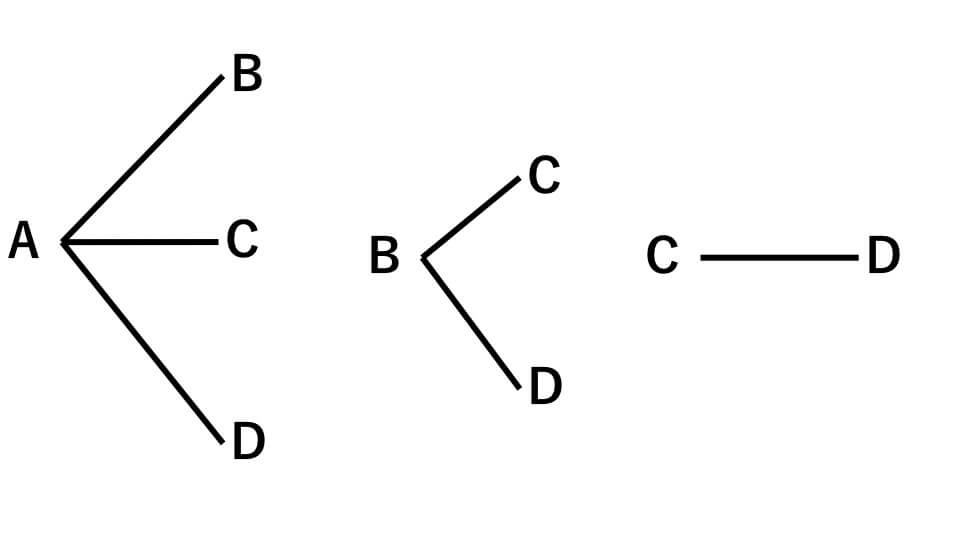
よって、答え　6通り

例題6

10円玉と50円玉と100円玉がそれぞれたくさんあります。これらを使って200円のお菓子を支払う方法は何通りあるか求めなさい。ただし使わない硬貨があってもかまいません。硬貨の枚数は限りがないものとします。

解説

100円と50円の硬貨の枚数が決まると、必然的に10円の硬貨の枚数が決まります。ですので、10円玉の硬貨の枚数を数える必要はありません。

硬貨の枚数の関係を表した表は下のとおりになります。

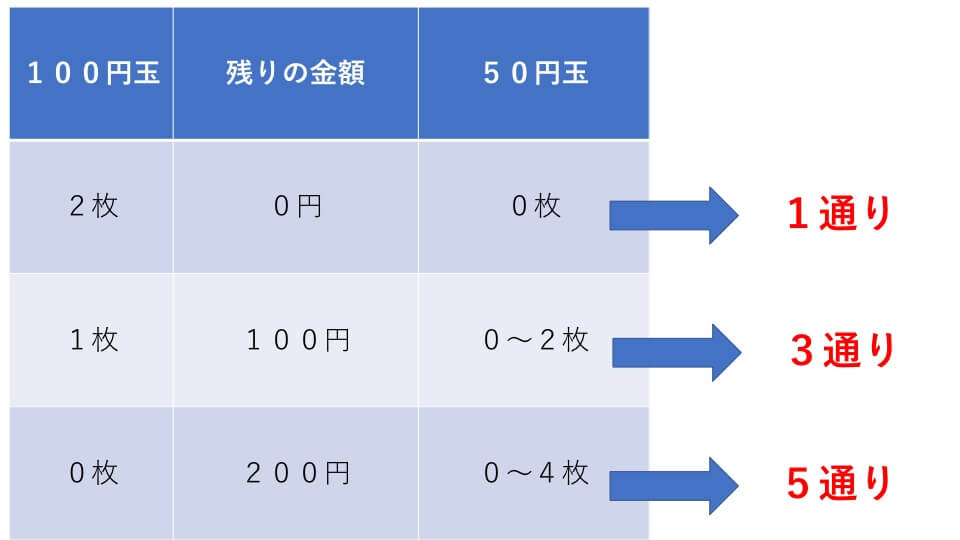
上の表より、全ての組み合わせは、

1＋3＋5＝9

よって、答え　9通り

まとめ

いかがだったでしょうか？中学受験の算数で出題される場合の数の問題は、樹形図や表を書いて求めれるものばかりです。とにかく場合の数の問題に出会ったら、樹形図や表を書いて考えてください。

樹形図や表を書くときは、綺麗に書くことは意識せずに自分がわかりやすくように書いてください。きれいに書くことにこだわり過ぎると時間がかかってしまいますので、そこは注意しましょう。

最後までご覧いただきありがとうございました。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】