中学受験 理科 ばねの学習ポイントと基本問題・入試問題を徹底解説

中学受験の理科で出題されるばねの問題は単純な暗記だけでは解きにくい問題が多いです。特に入試問題ではばねの性質や力と重さの関係を十分に理解できていないと解けない問題がほとんどです。入試ではそれらの性質を理解した上で計算を解く思考力が求められます。

この記事では、力と重さ、ばねの性質からわかりやすく解説していますので、理科が苦手な人、ばねの問題を始めて勉強するという人でも、ばねの学習のポイントが分かります。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

そもそも重さとは？

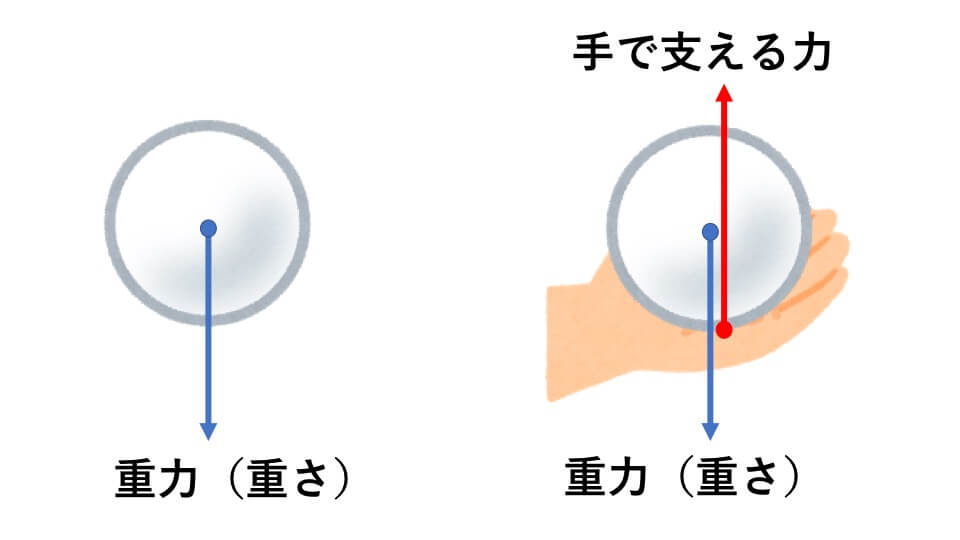
日常生活で何かものを手に乗せると重く感じると思います。また手からものを離すと、ものは地面に落ちてしまいます。これはものを下に引っ張ろうとする力が働いているからです。地球上の物質には、全て地球の中心に引っ張ろうとする力が働きます。地球がものを引っ張る力のことを重力、その大きさのことを重さと言います。基本的な用語なので必ず覚えてください。

ばねの性質

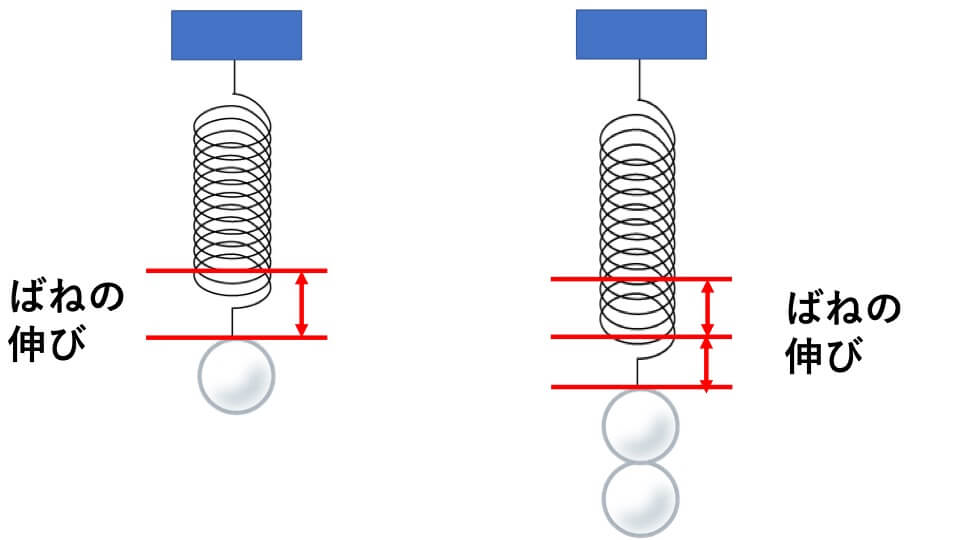
ばねは、引っ張ったり、押し縮められたりすると、元に戻ろうとする力が働きます。このような性質を弾性と言います。そしてこの弾性を利用してクリップやばねばかりなどの道具が作られています。

ばねの伸びは吊り上げたものの重さに比例します。つまり、物の重さが重ければ重いほどばねは伸びていくということです。これをフックの法則と言います。この法則はばねの問題を解く上で大変重要になってくるので必ず覚えてください。

ばねの直列つなぎと並列つなぎを解説

ばねの直列つなぎ

直列つなぎとは、同じ伸び方をするばね2本をつなぎます。このときのばねの重さは0として考えます。下の図を見てください。

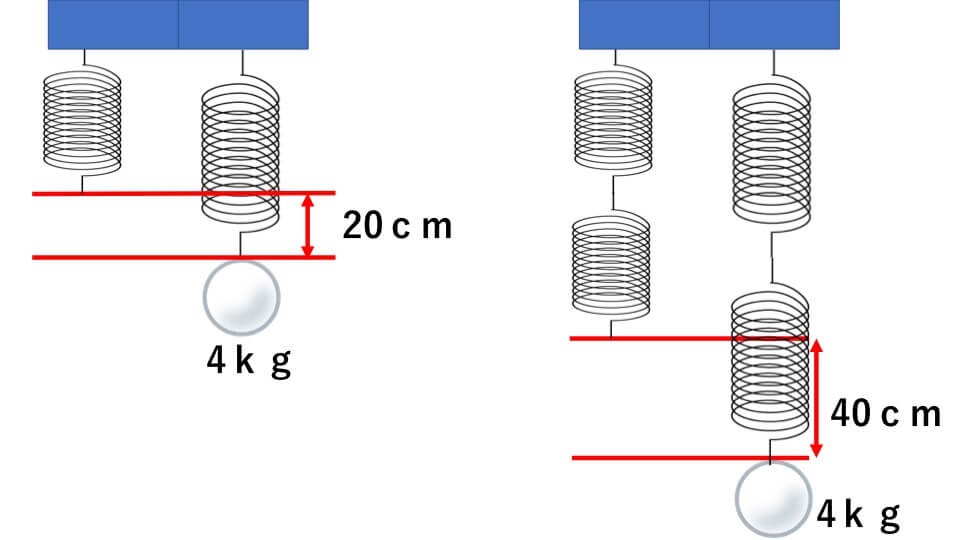
普通に4kgの重りをばねにつなぐとばねの伸びは20cmです。しかし直列つなぎにするとばねの伸びは40cmになります。これは上のばねは4kgの重りを支えることになり、4kgの重りの分だけ伸びます。また下のばねも4kgの重りをつけているのでその分だけばねは伸びます。ですので、ばね全体の伸びは1本のときと比べて2倍の伸びになります。つまり、ばね全体の伸びはばねの本数に比例することがわかります。

ばねの並列つなぎ

並列つなぎとは、同じ伸び方をする2本のばねを並列につないで重りを吊り上げます。下の図を見てください。

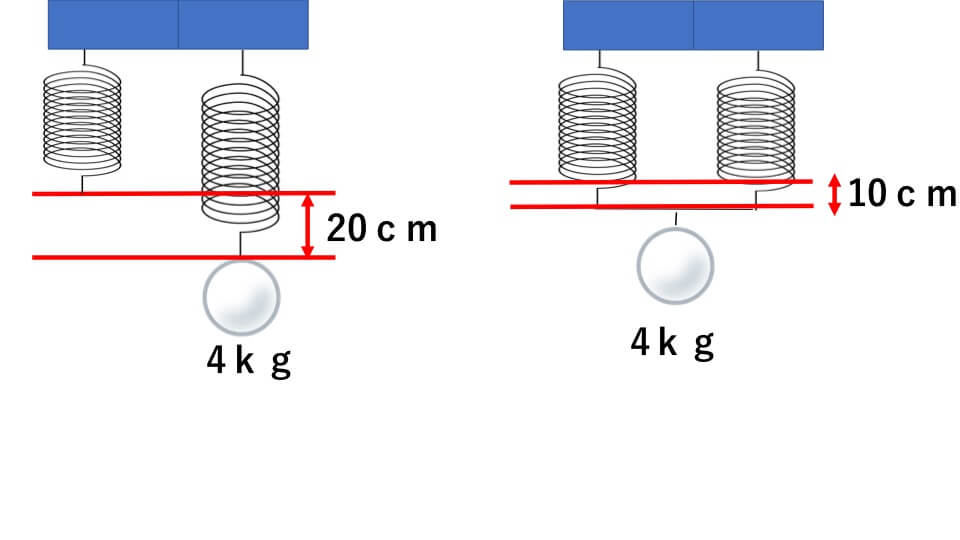
それぞれのばねは半分の大きさの重さを分担して支えることになります。ですのでばねにかかる重さとばねの伸び方は、1本で支えるときの半分(1/2)になります。また、ばねを3本、4本と増やしていくと1/3、1/4の大きさの重さを支えることになるので、ばねの伸び方も1/3、1/4となります。つまりばね1本の伸びはばねの本数に反比例することがわかります。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

ばねの基本問題にチャレンジしてみよう！

例題1

下の図を見てください。右側、左側共に同じ伸び方をするばねを使用しています。左側のばねには5kgの重りがかかっています。そのときのばねの伸びは7cmでした。右側のばねには8kgの重りがかかっています。このときの右側のばねの伸びは何cmですか。

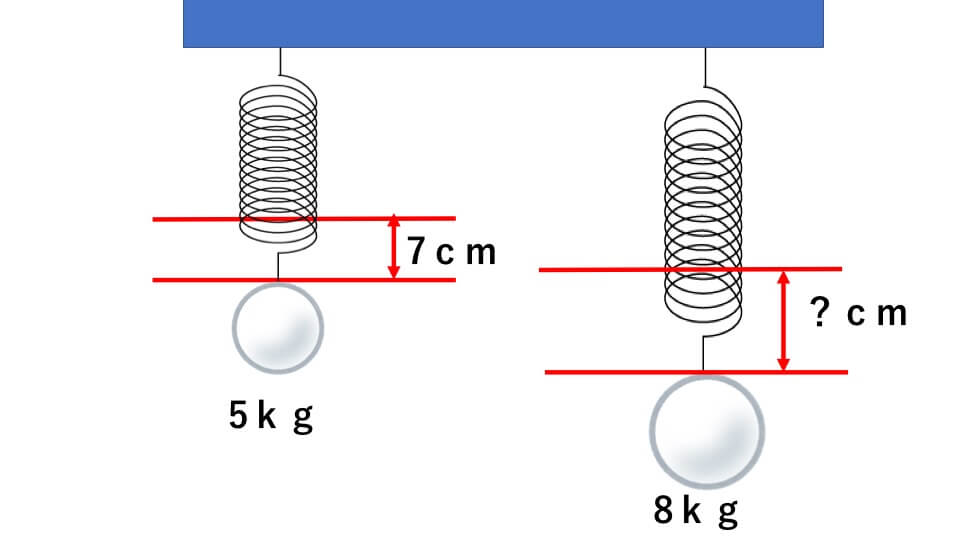
解説

ばねの伸びは、吊り下げた物の重さに比例するという性質(フックの法則)を利用して考えます。

求めたいものは左側のばねの伸びなので、右側のばねの伸びをxとして比例式を作ります。

5:7＝8:x 比の式は内同士と外同士をかけて求めるので、

5x＝56

x＝56÷5

x＝11.2

よって答え　11.2cm

例題2

3Nの力を加えたら8cm伸びるばねに6Nの力を加えたら何cm伸びるか求めなさい。

解説

これも例題1と同じ考え方でフックの法則を利用して考えます。6Nの力を加えたときのばねの伸びをxとして考えて比例式を立てると、

3:8＝6:x

3x＝48

x＝16

よって答え　16cm

例題3

ばね1本に2kgの重りを吊り下げているときのばねの伸びは20cmでした。これと同じばねを2本使って直列つなぎした場合のばね全体の伸びは何cmになるか求めなさい。

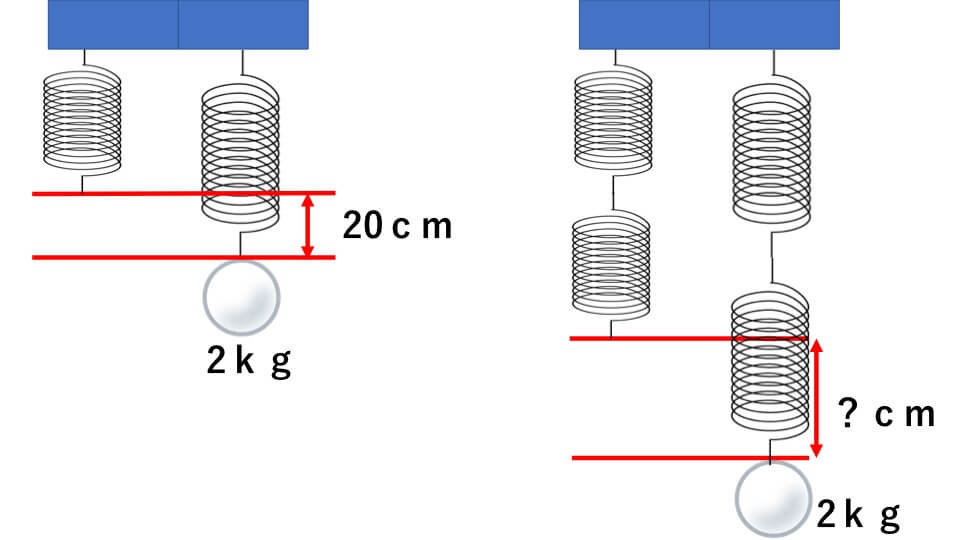
解説

直列つなぎの場合のばね全体の伸びは、ばねの本数に比例するという性質を使い考えます。今回使用しているばねは2本なので、ばねの全体伸びは2倍になることがわかります。ですので式は

20×2＝40

答え　40cm

例題4

ばね1本に3kgの重りを吊り下げているときのばねの伸びは30cmでした。これと同じばねを2本使って並列つなぎした場合のばね全体の伸びは何cmになるか求めなさい。

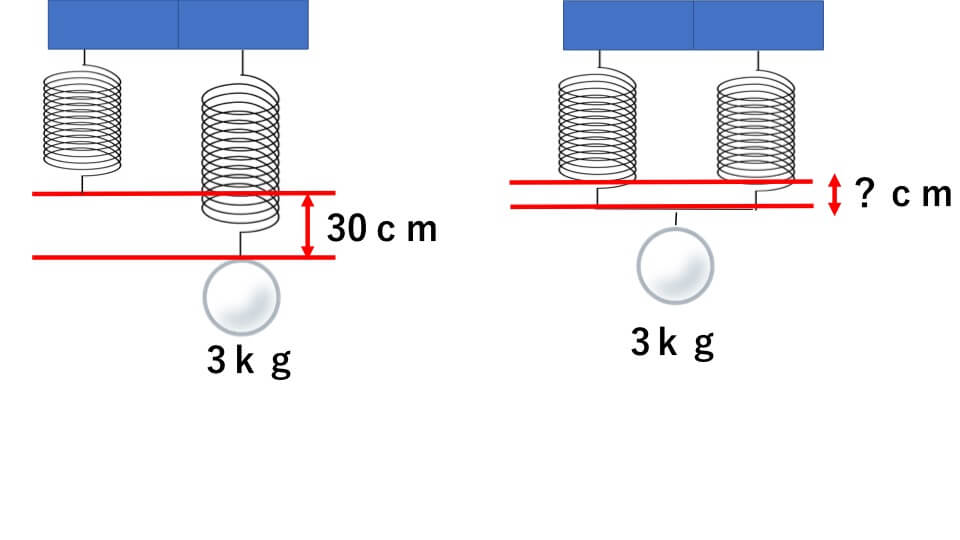
解説

並列つなぎの場合のばね全体の伸びは、ばねの本数に反比例するという性質を使います。今回使用したばねは2本なので、ばね全体の伸びは1/2倍になることがわかります。ですので式は

30×1/2＝15

答え　15cm

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

ばねの入試問題にもチャレンジ【応用編】

ここからは、実際の入試問題も紹介します。中学受験で出題されるばねの問題は、ばねの性質や力と重さの関係を十分に理解できていないと解けない問題がほとんどです。

また十分な解説がなければ、小学生には理解しづらいかと思います。そこで今回は実際の入試問題を使用してばねの問題を解説していきます。

• 理科の難しいばねの問題が解けるようになりたい
• ばねの問題が苦手
• 中学受験を考えている

このような人は是非今回の記事を参考にして、下記の実際の入試問題を解いてください。

問題1

おもりをつけないときの長さ(自然長)が20cmで10gのおもりをつけると1cm伸びるバネがあります。このバネを使い、厚さが一定の薄い板を天井からつり下げる実験を行いました。

バネを2本使い、重さが80gの正方形の板を下の図のようにからつり下げました。この時、バネの長さは何cmになりますか。ただし、バネは斜めになったりせず、真下に伸びています。【暁星中　改】

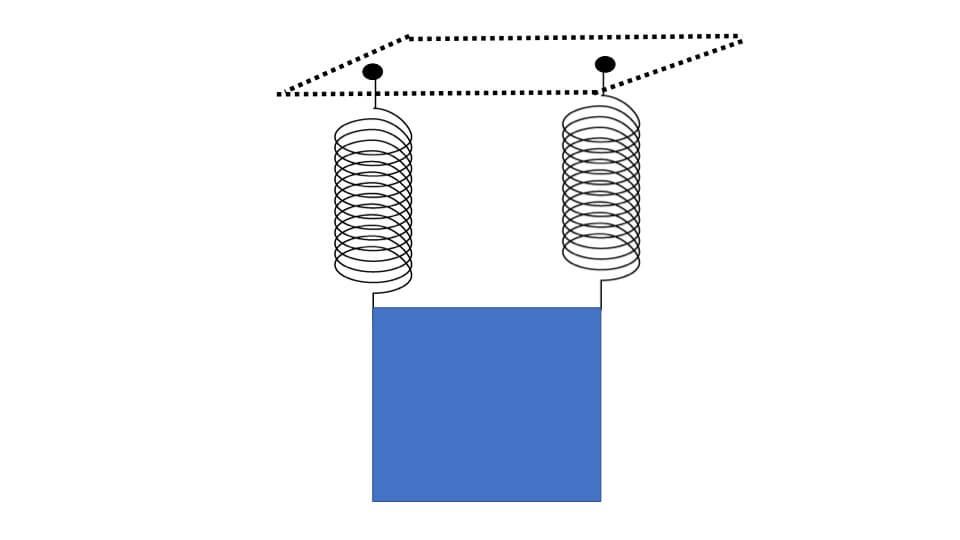
解説

この問題はバネを2本束にしてつなぐ、並列つなぎの問題です。それぞれのバネは1/2の大きさの重さを分担して支えることになるため、1本のばねが支えている重さは、

80×1/2＝40g となります。

このバネは10gのおもりをつけると1cm伸びるので、40gのおもりをつけたときの伸びをxとして求めると、

10:1＝40:x

10x＝40

x＝4cm となります。

この問題ではバネの伸びを聞いているのではなく、バネの長さを聞いているので、元々のバネの長さにバネの伸びの長さを足すことで求めることができます。よって式は、

20+4＝24

よって答え　24cm

問題2

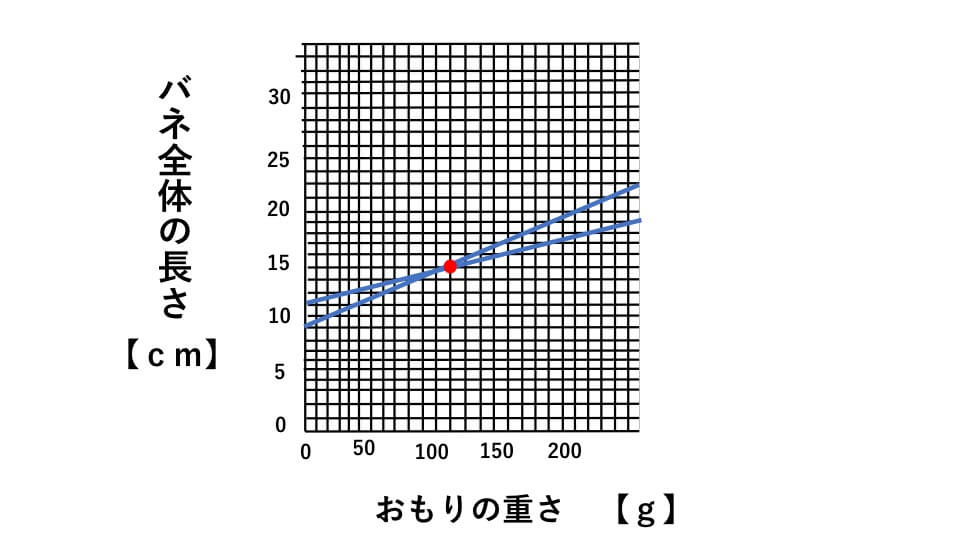
おもりの重さに比例して伸びるバネA、Bのバネ全体の長さの関係は下のグラフようになっています。赤点は交点を示しています。

今、下の図のようにバネA、バネBの長さ36cmの棒をつけ、棒の中央におもりつるしたところ、棒はちょうど水平になりました。棒とバネA、Bの重さは共に無視できるものとします。次の問いに答えなさい。【大阪星光学院中】

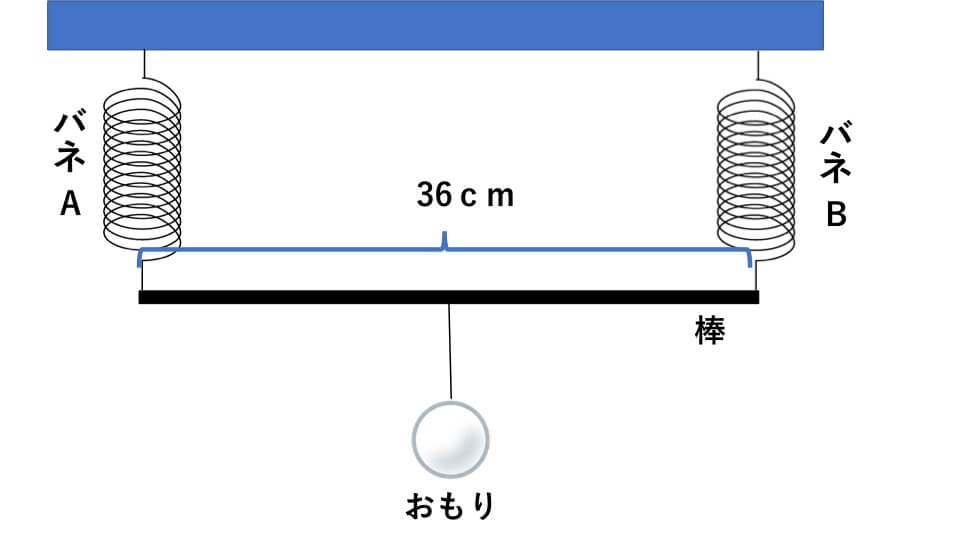
• (1) おもりの重さは何gですか。
• (2) バネAの伸びは何cmですか。
• (3) おもりの重さを変えて棒のある位置にすると、バネA、Bの長さが共に17cmになって棒が水平になりました。おもりの重さは何gですか。

(1)解説

棒がちょうど水平になったということは、バネAとバネBの長さが等しいということになります。グラフよりおもりの重さが120gのときにバネ全体の長さがいずれも15cmになっています。この時バネA、バネBの両方に120gの重さがかかっているということがわかります。ですのでおもりの重さは、

120×2＝240

答え　240g

(2)解説

グラフより、おもりの重さが0g、つまり重りがない状態でのバネAの長さは9cmです。また120gのおもりがかかったときのバネAの長さは15cmです。つまり伸びた後の長さから伸びる前の長さを引けば、伸びた長さがわかるので、式は、

15-9＝6

答え　6cm

(3)解説

グラフよりバネA、バネBの長さが17cmになっているときのおもりの重さを見ると、バネAには160g、バネBには200gの重さがかかっているので、おもりの重さは、

160＋200＝360

答え　360g

問題3

長さが同じで材質の違うバネAとバネBに長さ1mの軽い棒をとりつけ、棒の中点に60gのおもりを吊すと、下の図（図１）のように棒が水平になりませんでした。

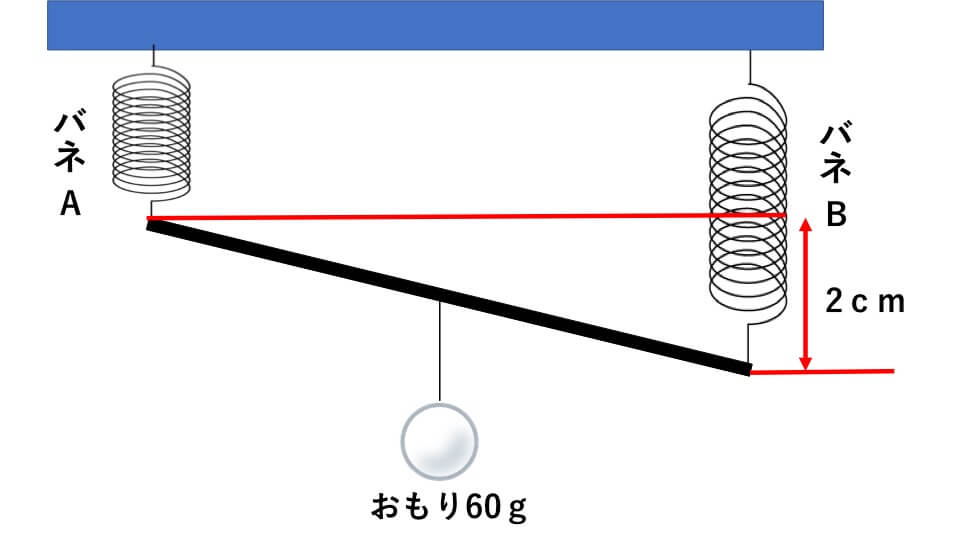
この時、バネAの真下に60gのおもりを吊すと、Aだけさらに2cm伸びて下の図（図2）のように棒は平行になりました。

次の問いに答えなさい。【愛光中】

• (1) 図1のとき、棒を水平にするには中点に吊るした60gのおもりをどこに移動すれば良いでしょうか。バネAの距離で答えなさい。
• (2) 図2のときバネBが天井を引く力はいくらですか。
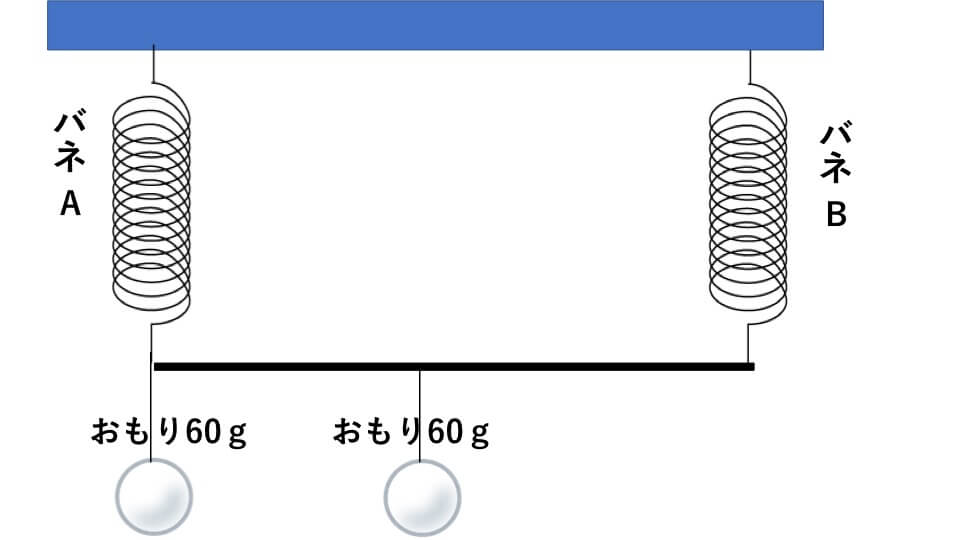
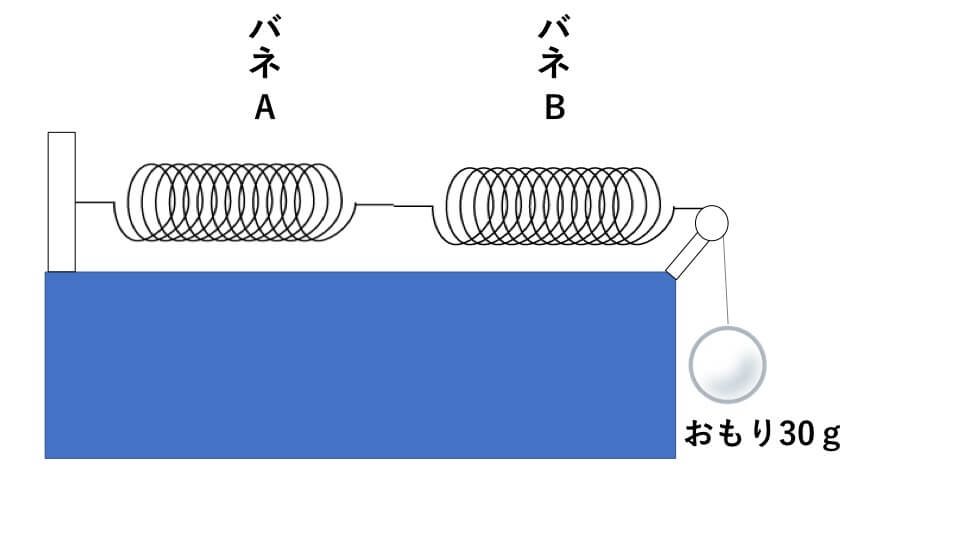
• (3) 下の図のように、バネAとバネBをつなぎ、30gのおもりを滑車を使って吊すと、バネBの伸びはいくらですか。

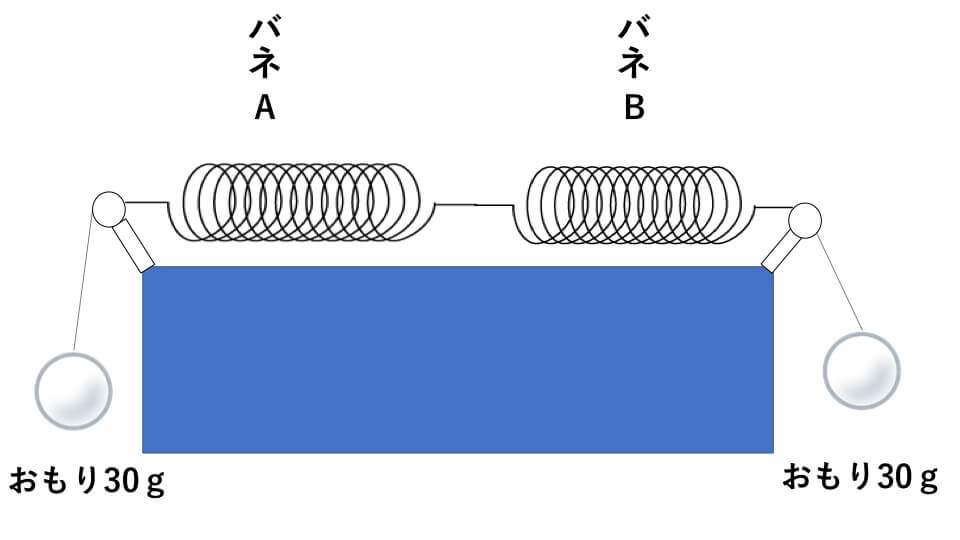
• (4) 下の図のように、バネの両側に30gのおもりを1個ずつ滑車を使って吊すと、バネAとバネBの伸びの合計はいくらですか。

(1)解説

図2からバネAは60gで2cm伸び、全体で3cm伸びています。ですのでバネAは30gで1cm、バネBは10gで1cm伸びるので60gを3:1の割合でかかるところに吊るせばいいです。棒の長さは1mなのでこれをcmに直すと100cm。100cmを3:1の割合で分けると、

100×1/（3＋1）＝25

答え　25cm

(2)解説

バネAの真下におもりを付けてもバネBにかかる重さは変わらないので、

答え　30g

(3)解説

直列につないだ場合は、両方のバネに同じように重さがかかるので、

答え　3cm

(4)解説

(3)の時と、バネにかかる力は同じなので、

1＋3＝4

答え　4cm

まとめ

いかがだったでしょうか？ばねの性質を根本から理解して問題を解けば、そこまで難しくないと感じてもらえたと思います。ただ単に暗記するのではなく、理屈をしっかりと理解してばねの問題は解くようにしてください。

また、後半で紹介しました実際の中学受験の入試問題ともなるとなかなか難しかったかもしれませんが、基礎から理解できていれば解けない問題ではありません。ぜひ、頑張って習得しましょう。

最後までご覧いただきありがとうございました。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】