中学受験の算数で出題される単元「立体図形」。教科書では平面であるため実際の立体図形を確認しづらく、中学受験生によって認識に差が出る単元でもあります。
直方体の体積はなぜ「たて×横×高さ」で求められるか理由までちゃんと説明できますか?中学生、高校生でも答えられない人が多いと思います。学校で公式を習ったからなんとなくその公式を使って覚えている人が非常に多いように感じます。公式を暗記して使うためには、なぜその公式になるのか考える必要があります。
今回の記事では、直方体の体積の公式が成り立つ理由から角柱と円柱の体積の求め方まで解説します。
- 算数が苦手な人
- 立体図形がイメージできない人
でもわかりやすく解説しているので、安心して最後まで記事を読んでください。
立体図形① 直方体とはそもそもどんな立体?
正方形だけで囲まれた立体図形、つまりサイコロのような形を立方体(りっぽうたい)と言います。また長方形だけ、もしくは長方形と正方形で囲まれた立体つまりテッシュペーパーの箱やダンボール箱のような形を直方体(ちょくほうたい)と言います。

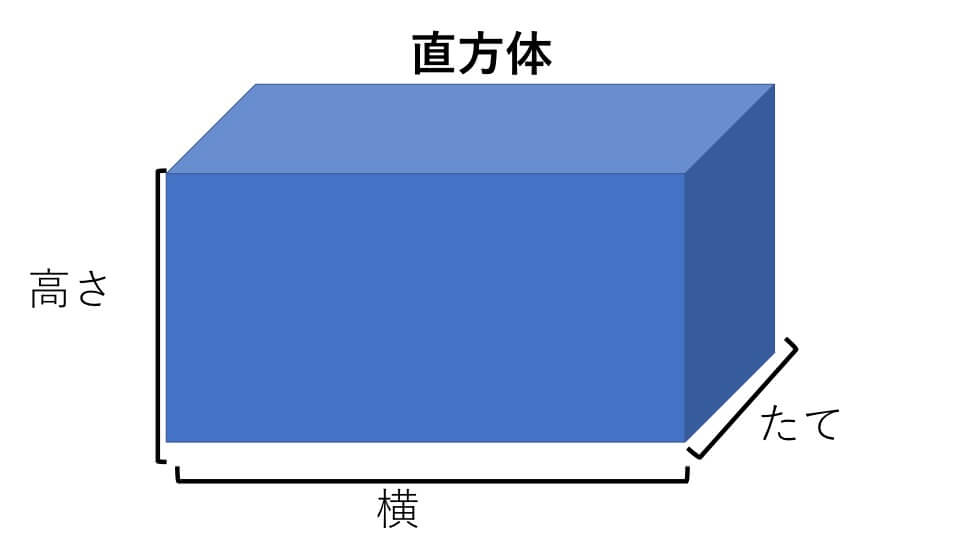
ここで立体の大きさのことを体積と言います。算数によく出題される体積の単位は㎤(立方センチメートル)です。1辺が1cmの立方体の体積が1㎤です。
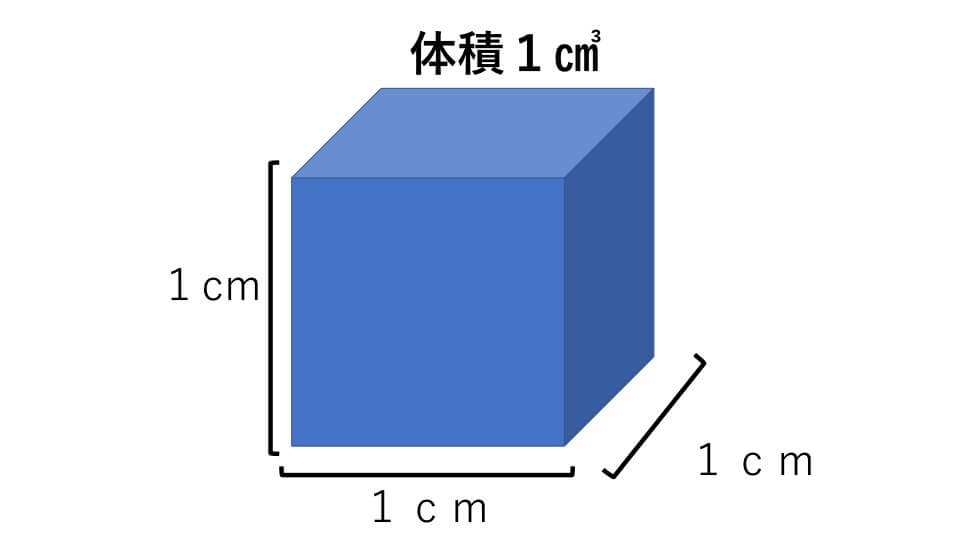
今から公式が成り立つ理由を説明する上で重要となりますので、必ず理解をしてください。
立体図形② 直方体の面積「たて×横×高さ」立方体の面積「1辺×1辺×1辺」が成り立つ理由
具体的な例題を使ってこの公式が成り立つ仕組みを解説していきます。
例題1
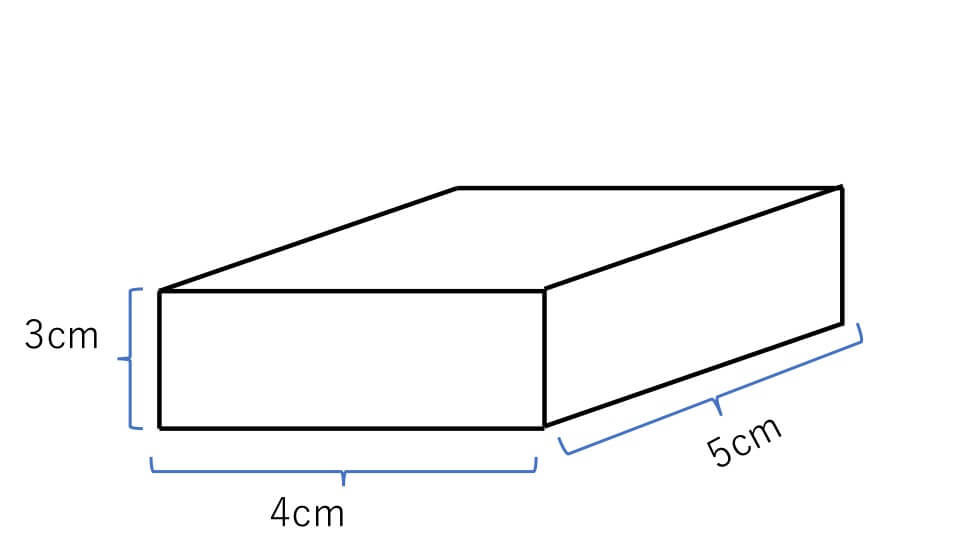
次の直方体の体積は何㎤ですか?
解説
この直方体の体積は、「たて×横×高さ=3×4×5=60㎤」と求めることができます。しかしどうして「たて×横×高さ」で求めることができるのでしょうか?
例題1の直方体を1辺が1cmの立方体に分けると下の図のようになります。
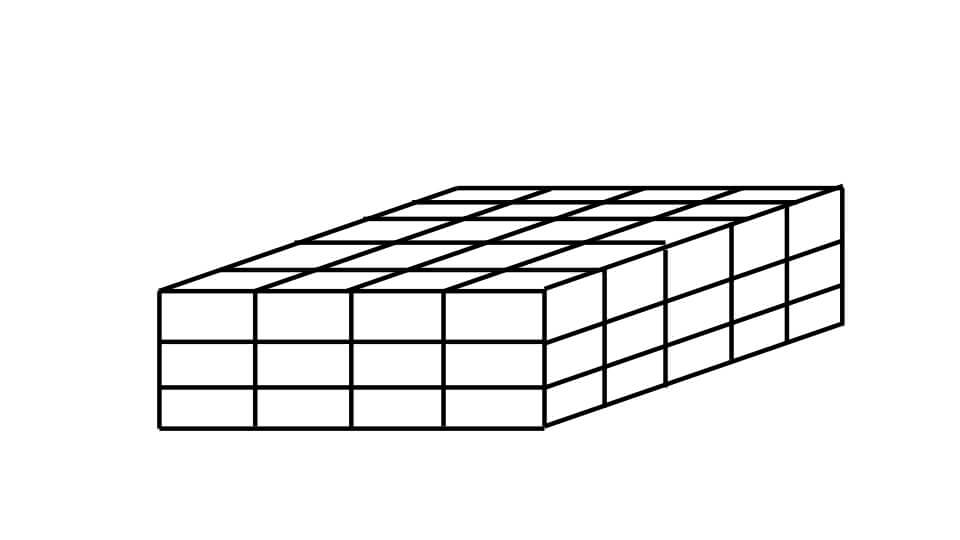
「1辺が1cmの立方体の体積は1㎤」であることは先程お伝えしました。ですので「例題1の直方体の中に1辺が1cmの立方体(体積が1㎤)がいくつあるのかを考えれば、直方体の体積を求めることができます。
下の図のように下から1段目のみ注目します。
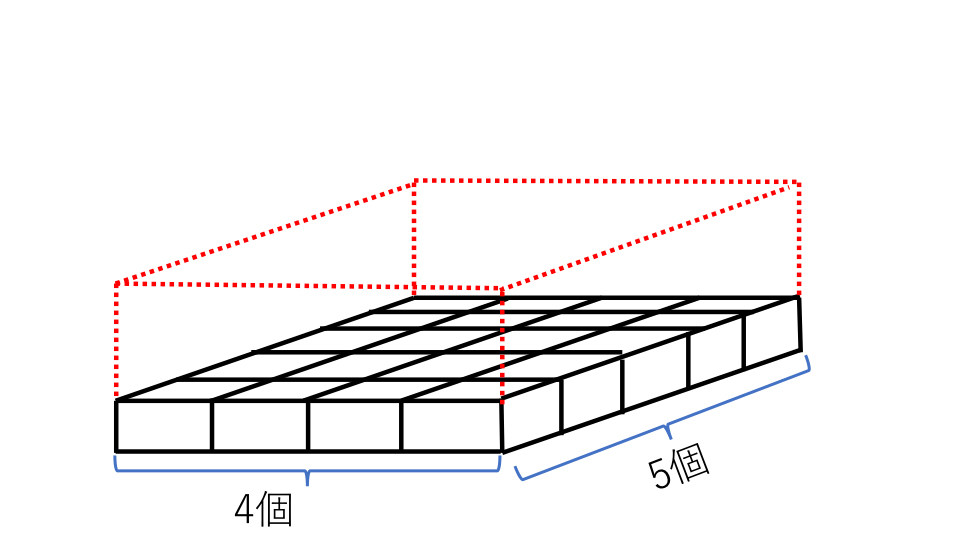
下から1段目には1辺が1cmの立方体が何個集まっているのか考えます。直方体のたてには5個、横には4個の立方体が並んでいることがわかると思います。ですので下から1段目には全部で5×4=20個の立方体が並んでいることがわかります。
そして、直方体の高さには3つの立方体が並んでいます。1段目に20個の立方体があり、それが3段あるということなので、全部で20×3=60個立方体があるとわかります。
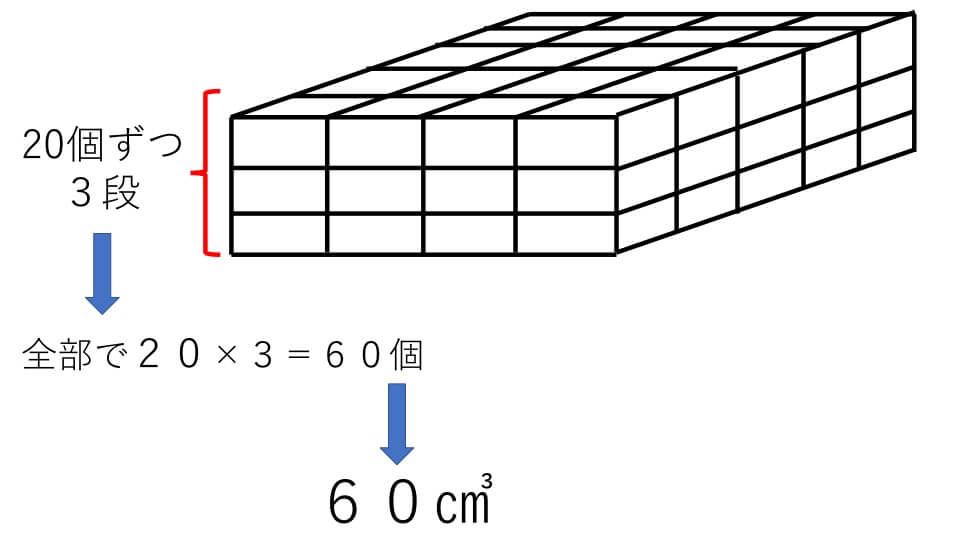
「1辺が1cmの立方体の体積が1㎤」でそれが60個あるので例題1の直方体の体積は60㎤と求めることができます。直方体のたて、横、高さに並んでいる立方体の数は「5個、4個、3個」とそれぞれの長さの数「5cm、4cm、3cm」は同じです。ですので直方体の体積は「たて×横×高さ」で求めることができるのです。
続いて立方体の体積が「1辺×1辺×1辺」が成り立つ理由について説明していきます。
同じように具体的な例題を使って説明していきます。
例題2
下の立方体の体積は何㎤ですか?
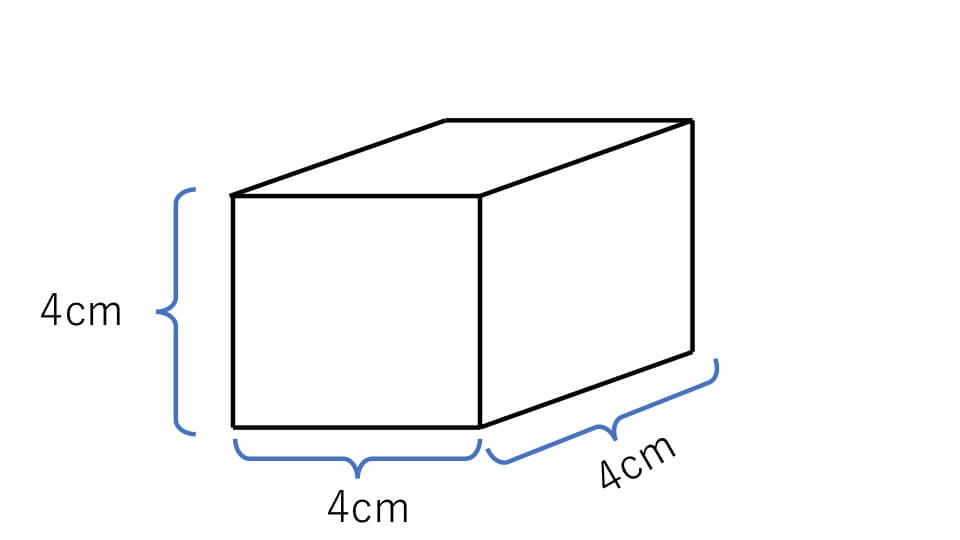
解説
この立方体の体積は「1辺×1辺×1辺=4×4×4=64㎤」と求めることができます。立方体が「1辺×1辺×1辺」で求めることができる理由も直方体の時と同じようにして説明できます。例題2の立方体を1辺が1cmの立方体に分けると下の図のようになります。
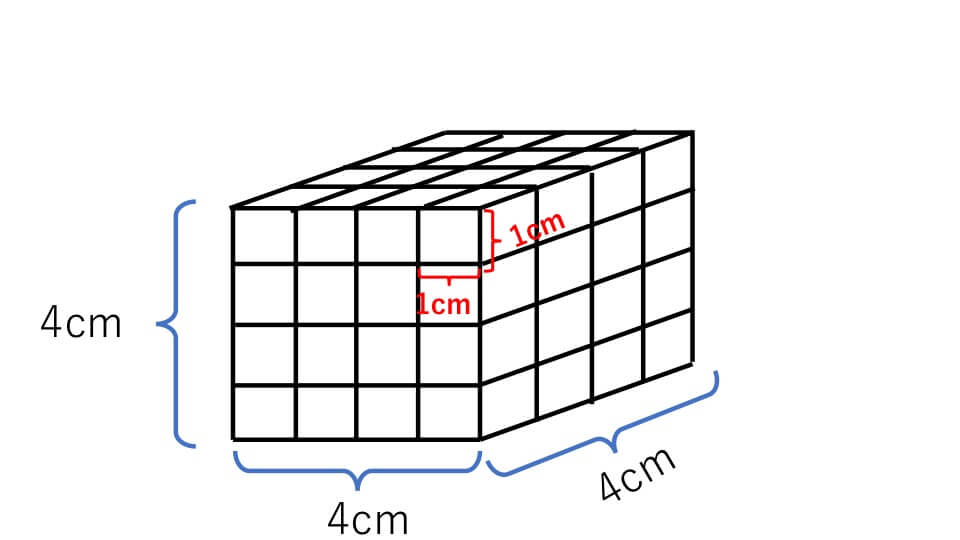
1辺が1cmの立方体は全部で4×4×4=64個あることがわかります。ですので例題2の立方体の体積は64㎤と求めることができます。
つまり立方体の体積は「1辺×1辺×1辺」で求めることができます。
立体図形③ 角柱と円柱とはどんな立方?
下の図のような立体図形を角柱、円柱と言います。
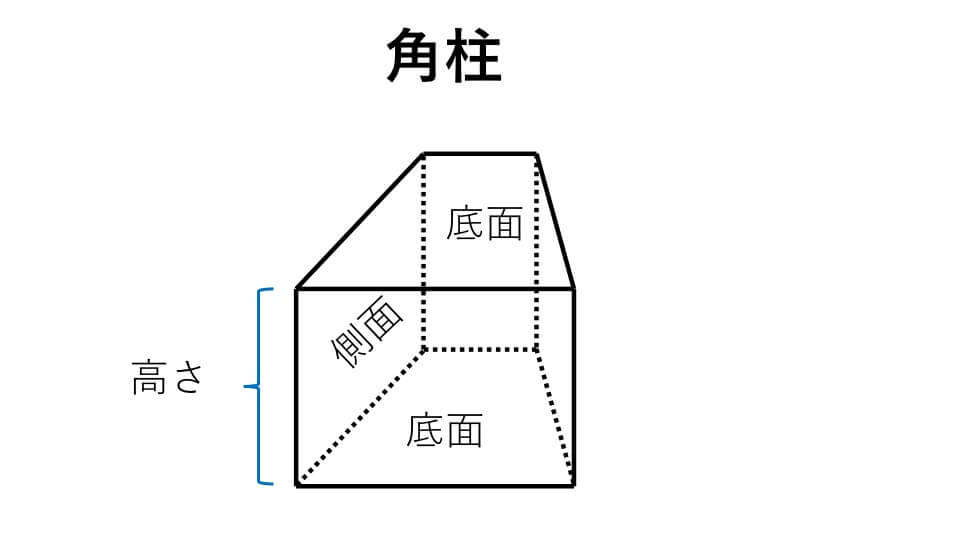
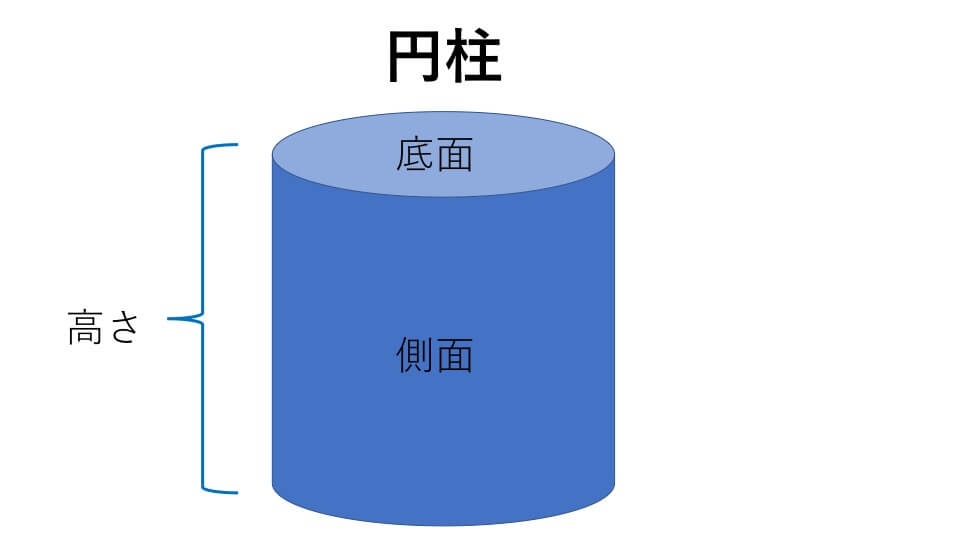
角柱と円柱で上下に向かい合う2つの面のことを底面(底面)と言います。そして1つの底面の面積のことを底面積と言います。また角柱では周りの長方形もしくは正方形のこと、円柱では周りの曲面のことを側面(そくめん)と言います。
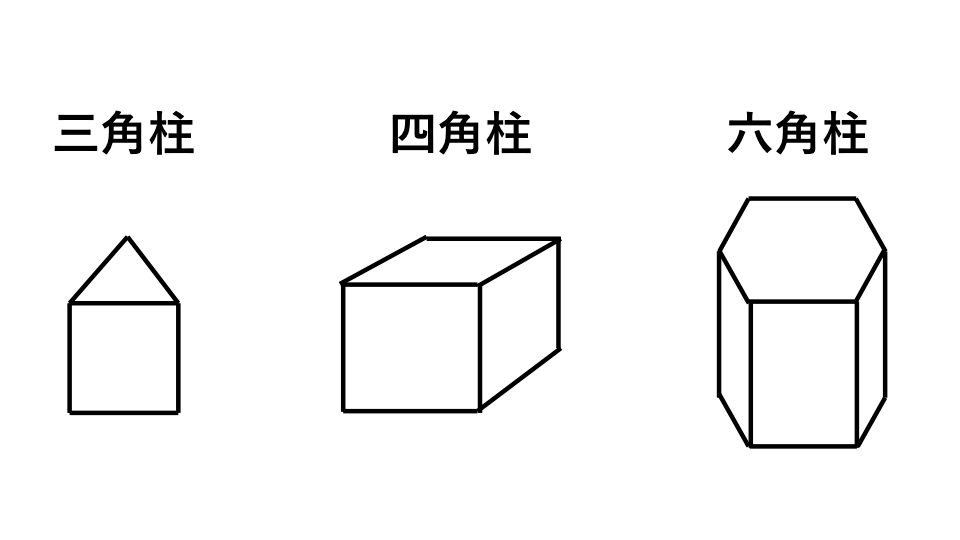
角柱の底面が三角形なら三角柱、四角形なら四角柱、五角形なら五角柱、六角形なら六角柱と言います。このように角柱は底面の形によって呼び方が変化します。
立体図形④ 角柱と円柱の体積の求め方
角柱もしくは円柱の体積=「底面積×高さ」
具体的な例題を使って公式の成り立ちを説明していきます。
例題3
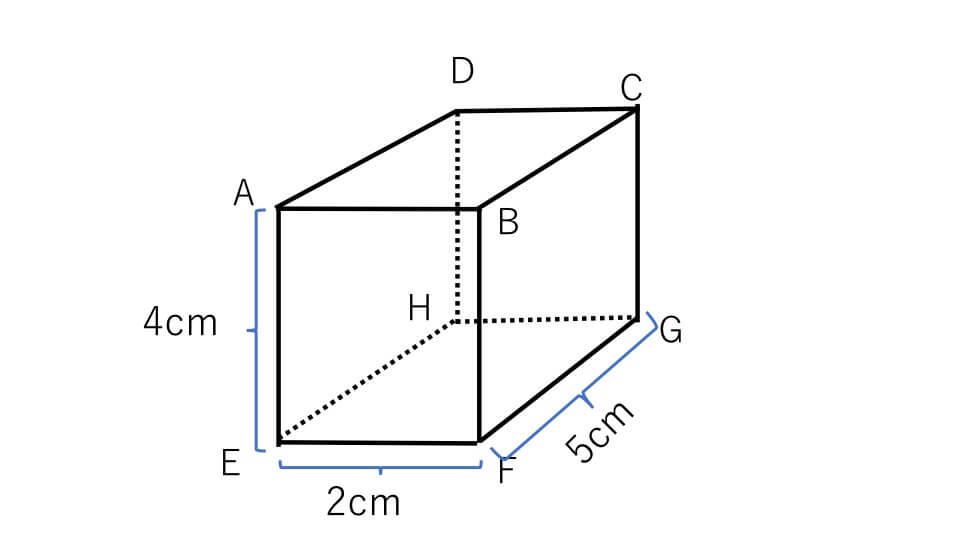
下の四角柱の体積を求めなさい。
解説
四角柱と言われていますが、これは先程説明した直方体のことです。直方体は四角柱の一種です。ですのでこの例題3の四角柱の面積は「たて×横×高さ=5×2×4=40㎤」と求めることができます。
ここで、この四角柱を下の図のように高さ1cmの部分に注目してみます。
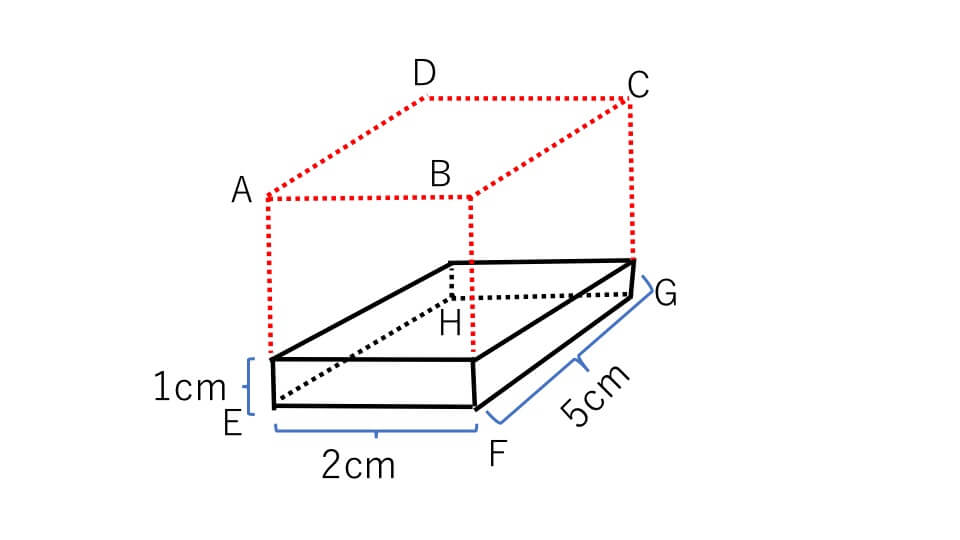
この部分の体積は「たて×横×高さ」で求めることができます。2×5×1=10㎤です。
ところで面EFGHを底面とするとき底面積は2×5=10㎠です。つまり高さ1cmの四角柱の体積(10㎤)と底面積(10㎠)はどちらも同じ数(10)になります。
そしてあらゆる角柱と円柱で高さ1cmの部分の体積と底面積は同じ数になります。ですので、角柱もしくは円柱の体積は「底面積×高さ」という公式で求めることができるのです。
例題3の四角柱なら底面を面EFGHとして考え面積を求めると2×5=10㎠で、それに高さをかけて10×4=40㎤と求めることができます。
例題4
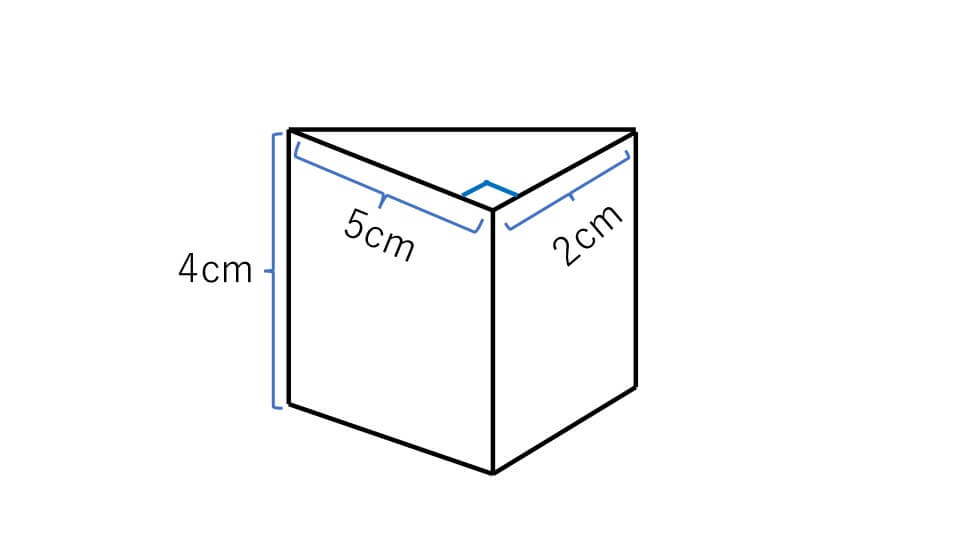
次の三角柱の体積を求めなさい
解説
底面は三角形なので、三角形の面積は「底辺×高さ÷2」で求めることができるので、5×2÷2=5㎠となります。
そして角柱の体積は「底面積×高さ」で求めることができるので、5×4=20㎤となります。
例題5
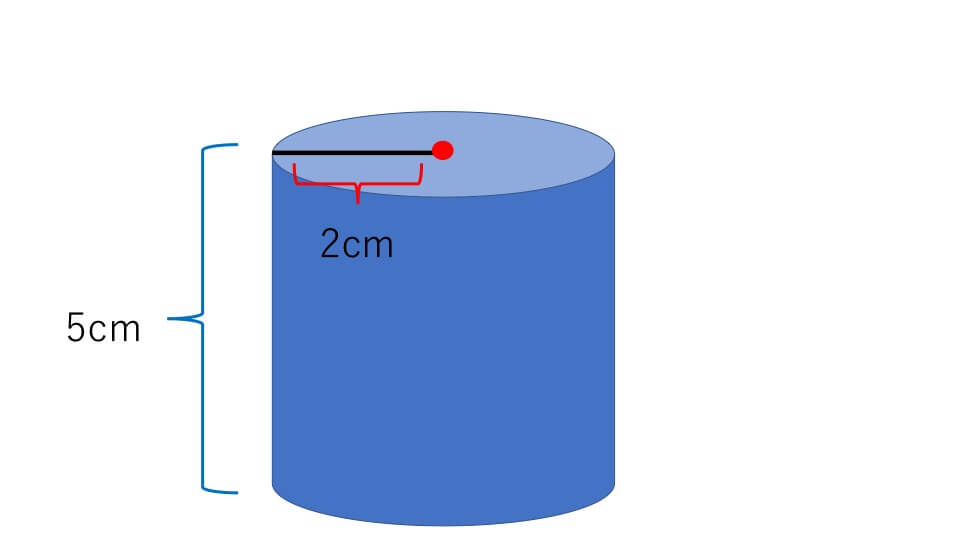
次の円柱の体積を求めなさい
解説
底面は円なので、円の面積は「半径×半径×3.14」で求めることができるので、2×2×3.14=12.56㎠となります。
そして円柱の体積は「底面積×高さ」で求めることができるので12.56×5=62.8㎤となります。
まとめ
いかがだったでしょうか?立体図形の体積の求め方を理屈から理解できたと思います。今回解説したやり方を身につけてお手持ちの問題集や参考書などで体積の問題を多く解いて自分のものにしてください。
次は回転体のポイント解説です。立体図形を理解した上で回転体の単元に進むことでより理解が進みます。

最後までご覧いただきありがとうございました。

