中学受験において『速さ』の問題は必ずと言っていいほど出題されます。『速さ』の分野をマスターすることで、これからの算数の学習がスムーズに進むことは間違いありません。また、速さをマスターすれば、中学受験だけではなく、高校受験でも大いに活躍する単元です。
また、速さが苦手な人に共通して言えることは、やみくもに公式を丸暗記して解こうとする子が多いですが、この記事では、ほとんど公式を使わずに『比』を使って解く方法をご紹介します。『比』を使うことで、公式に頼るのではなく、文章をしっかりと読むようになります。そうすれば、応用問題でも解けるようになります。
この記事を読むことで、速さの問題で苦手意識はなくなり、算数の速さを得点源にして今後の学習をより良いものにしていきましょう。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
そもそも速さって何?
「速さ」とは「一定の時間あたりに進む距離(長さ)」のことを言います。
速さの単位は次のような言葉で表します。
- 1秒間で進む距離(長さ)=秒速、毎秒
- 1分間で進む距離(長さ)=分速、毎分
- 1時間で進む距離(長さ)=時速、毎時
具体的に説明をすると、
- 1分間に30m進むなら「分速(毎分)30m」
- 1時間に1800m進むなら「時速(毎時)1800m」
となります。
これらの言葉の意味を必ず覚えてください。中学生や高校生でもはっきりと言えない人がいますが、これから速さの勉強をしていく上での基礎となります。
秒速から分速、時速と比を使って求める方法
速さの問題で、単位が統一されていないことがよくあります。その時のために単位を変える計算方法を知っておくようにしましょう。
学校では下のような図を作って、公式を覚えさせるのではないでしょうか?
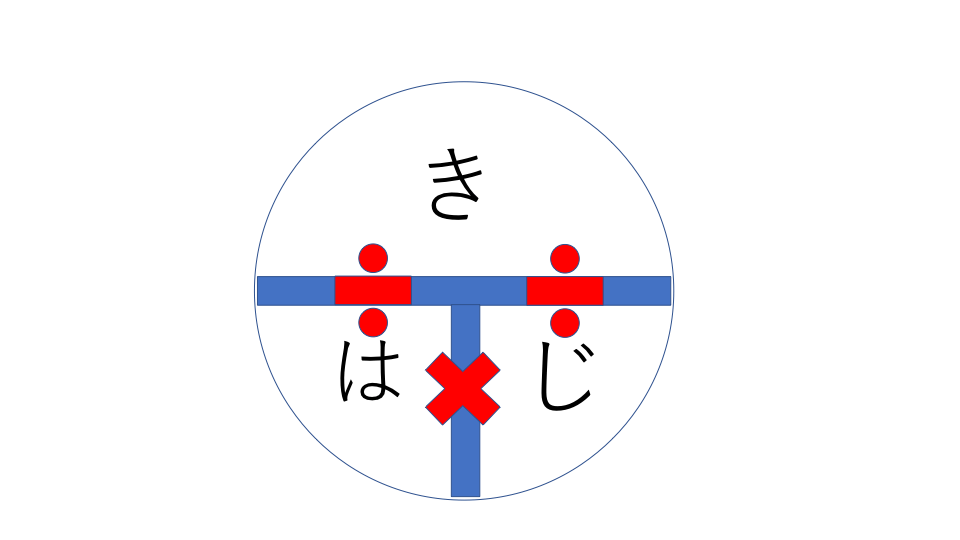
これは
速さ=距離÷時間
- 速さ=距離÷時間
- 時間=距離÷速さ
- 距離=速さ×時間
という風に求められます。ただ先生に教えられたから使っている人が多く、本質を理解していない生徒が非常に多いです。この方法でもいいのですが、図の書き方や図の意味を理解していないと、テストでは使えません。
今回はこの方法ではなく『比』を使った求め方で答えを導き出していきます。
例題
例題1)から解説していきます。まずは比を作ります。
秒速の意味を思い出してみてください。
秒速は「1秒間に進む距離」のことでしたよね。なので今回の問題では秒速50mとなっているので、1秒間で50m進むということです。
問題では分速を求めたいので、「1分間に進む距離」が知りたいです。1分間は60秒間なので、「60秒間に進む距離」と言い換えることができます。なので求めたい距離をxとして比の式を立てると
1秒間で50m=60秒間でx m
1秒間:50m=60秒間:x m
1:50=60:x
という式が成り立ちます。
後は内同士、外同士をかけて 3000=x と式を変形させて答えは分速3000mと求めことができます。
同じようにして、例題2) 1時間は60分なので
1:100=60:x
x=6000 答え時速6000m
例題3) 1時間は3600秒なので
1:20=3600:x
x=72000 答え時速72000m
となります。
このように比を使えば、公式を覚えていなくても簡単に単位の変換ができるようになります。そのためには、単位の意味をしっかりと覚えるようにしてください。
旅人算の基本の2パターン
速さの問題で頻繁に出題されるのは旅人算です。旅人算とは「登場人物が複数いる問題」にことを言います。登場人物が複数いることで、「出会い」や「追いかけ」といったパターンの問題ができます。
基本的には登場人物が2人いて、2人の速さの「和」か「差」について注目して解くことがほとんどです。登場人物が3人、4人と増えたとしても、2ずつ考えていくことで、答えを見つけることができます。
出会いの基本パターン
離れた2地点から向かい合って進んだ時に、いづれは二人が出会うことになります。このとき2人の速さと、出発してから出会うまでの時間や進んだ距離などの進行状況を考えていきます。
例題1)
お兄ちゃんと弟が5km離れた地点から向かい合って同時に出発しました。お兄ちゃんは分速65m、弟は分速35mで歩いています。2人が出会うのは出発してから何分後ですか?
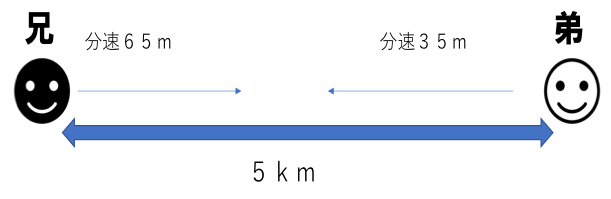
解説)
兄と弟が同時に出発しているので、1分間に65+35=100(m)ずつ近づいていく。つまり分速100mと同じ意味合いになる。
5km=5000mで 求めたいものは時間なのでxとすると
1分間:100m=x分間:5000
1:100=x:5000
100x=5000
x=50 答え50分後
となります。
追いかけの基本パターン
離れた場所から同じ方向に進んで場合に「追いかけ」が発生します。二人の速さに差があると必ず追いつくことになります。
このときの二人の速さと出発してから追いつくまでの時間や進んだ距離などの進行状況を考えていきます。
例題2)
600m先を分速35mの速さで歩いている弟を、お兄ちゃんが分速65mの速さで追いかけます。お兄ちゃんが弟に追いつくのはお兄ちゃんが出発してから何分後ですか?
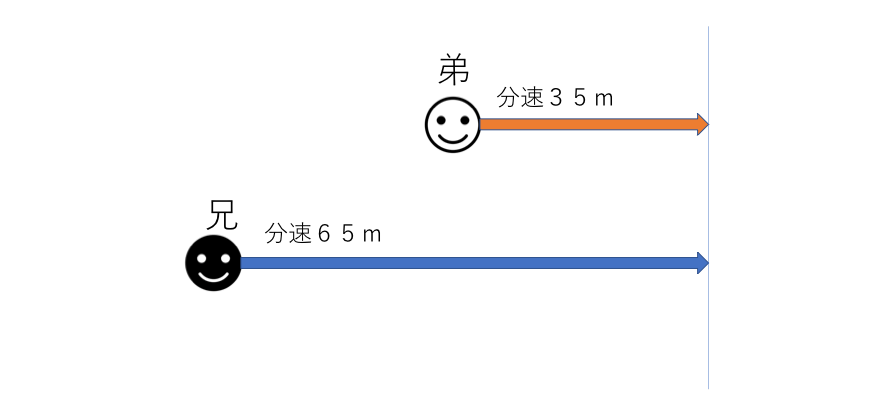
解説)
1分間に、65ー35=30(m)ずつ近づいていく。つまり分速30mで兄は弟に近づいていくことになる。
兄と弟の距離は600mで、求めたいものは時間なのでxとすると
1分間:30m=x分:600m
1:30=x:600
30x=600
x=20 答え20分
次の問題はひっかけ問題です。引っかからないように注意してください。
例題3)
お兄ちゃんと弟が公園を同時に出発し、公園から2km離れたところにある秘密基地へ向かいました。お兄ちゃんは分速65m、弟は分速35mで歩き、秘密基地に着いたらそのまま休まず公園に引き返します。お兄ちゃんと弟が初めてすれ違うのは、出発してから何分後ですか?
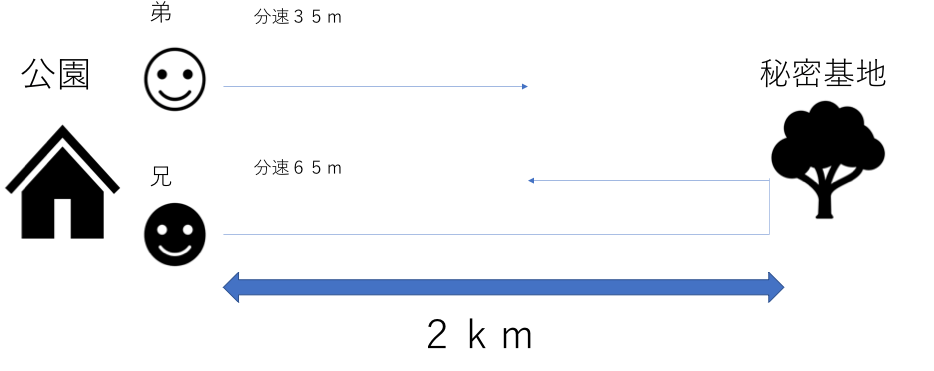
解説)
上の図で考えると兄が引き返してから出会うので、二人が進んだ距離の和が、2×2=4(km)とわかる。4km=4000m
例題1と同じ考え方で、1分間に65+35=100(m) 進むことがわかる。これを比の式に表すと
1:100=x:4000
100x=4000
x=40 答え40分後
3人の旅人算の基本パターン
旅人算の問題の中で、登場人物が2人ではなく3人や4人になることがあります。登場人物が3人の旅人算を「3人旅人算」と言います。
この3人旅人算でよく出題される問題が次のような問題です。
例題4)
1分の道に沿ってA地点とB地点があります。A地点からお兄ちゃんと弟がB地点からお父さんが同時に出発し、向かい合って進みました。お兄ちゃんとお父さんがすれ違ってから5分後に弟とお父さんがすれ違いました。お兄ちゃんは分速85m、弟は分速35m、お父さんは分速95mで歩いていたとすると、A地点とB地点は何km離れていますか。
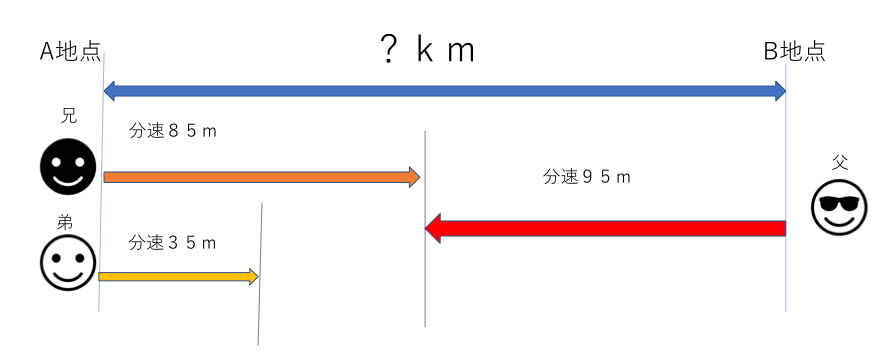
解説)
まずは問題文の状況を上の図のように書きましょう。
「弟と父が5分で出会う距離」に注目してください。この距離は「兄と弟の進んだ距離の差」と等しいことがわかるかと思います。
なので兄と弟の進んだ距離の差は
1分間に弟と父が進む距離は35+95=130mで
1:130=5:x
x=650 となり 650mとわかる。
兄と父が出会った時間を求めると
兄と弟の速さの差は分速、85-35=50(m)なので
1:50=x:650
50x=650
x=13 13分間で兄と父が出会ったとわかる。
よってA地点とB地点の距離は兄と父が13分間歩いた距離を求めるで導き出せる。
1分間で85+95=180(m)進むので
1:180=13:x
x=2340 答え2340m
応用問題
これまで、問題を4題解いてきましたが、いかがだったでしょうか?
公式を覚えずに「比」を使った計算方法で速さの問題が解けることがわかったと思います。
文章をしっかりと読んで、比を使えば難しい問題でも解けるようになります。
次は応用問題に挑戦してみましょう
例題5)
5/20日、お兄ちゃんは1週3000mのコースでランニングを始めました。弟は同じコースを逆周りにランニングすることにしました。弟とは毎回10分ごとにすれ違います。5/21日、お兄ちゃんは少し気分を変えたいと思い、いつもと逆にランニングを始めました。弟昨日と同じようにランニングしています。今日はお兄ちゃんが50分おきに弟に抜かされました。お兄ちゃんと弟の速さは、それぞれ分速何mですか?
解説
5/20日と5/21日を分けて考えます。
5/20日
下の図のように表されます。
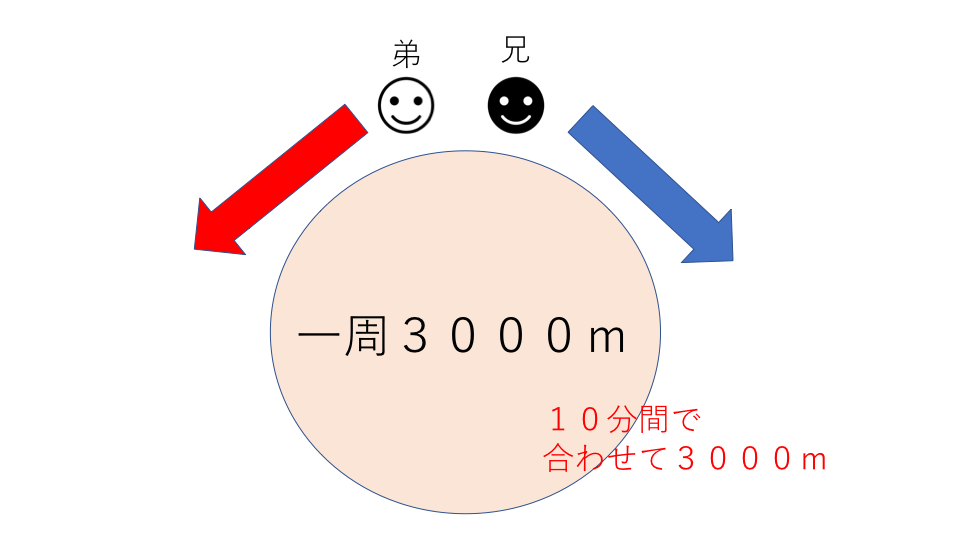
10分おきにすれ違うので10分で二人合わせて3000m進んでいることなります。
比を使って1分間当たりの二人の進む距離を求めると、
10分:3000m=1分:x m
10:3000=1:x
3000=10x
x=300
つまり1分間当たりの二人の進む距離は300mです。
5/21日
兄と弟は同じ方向に走っています。兄は50分で周回遅れにされるので、弟は50分で兄よりも3000m多く進んだことになります。これを1分間あたりに進んだ距離を求めると。
50分:3000m=1分:x m
50:3000=1:x
3000=50x
x=60
つまり、1分間に進む道のりの差は60mです。
言い換えると1分間で60m弟の方が進んでいると言えます。
下の図のようになります。
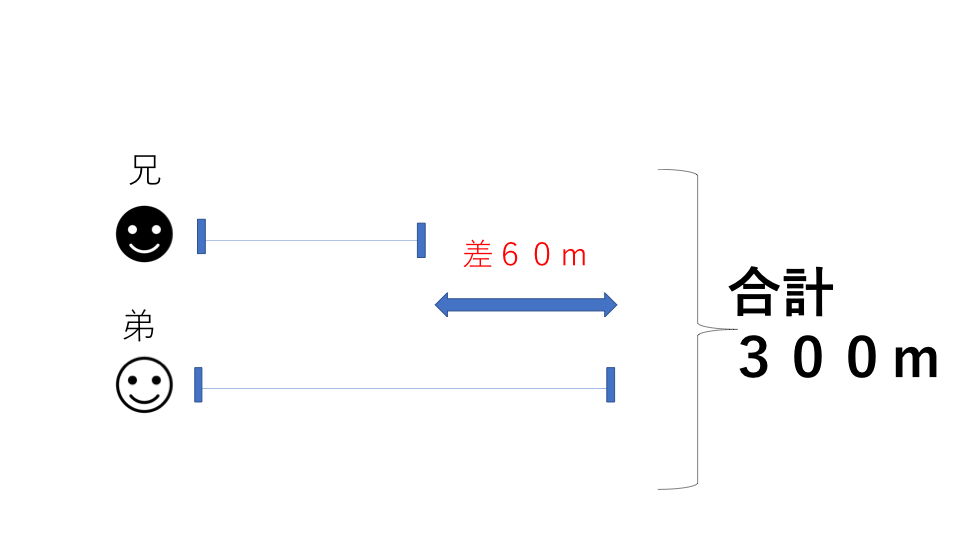
この図から
(300+60)÷2=180(m)
そのため弟が1分間に進む距離は180m。
お兄さんは1分間に進む距離は
180-60=120m
よって答えは
お兄ちゃん120m
弟 180m
最後の問題はあえて弟の方が速く進むように設定しました。今までの問題では弟の方が遅かったので、「なんだかおかしいかも」と思った人がいるかもしれません。
算数の問題では、自分の感覚や変な先入観を持って数学の問題は解かないようにしましょう。
まとめ
いかがだったでしょうか?比を使って、速さの単位を理解することで、公式を覚えなくても速さの問題を解けることが理解できたと思います。
記事中では画像を用いて説明することが多かったですが、実際に問題を解くときも、図を書いてイメージするようにすると問題を理解しやすいことが多いです。イメージして理解することで、文章の本質が見えてきます。
算数はパターンで覚えるのではなく、どうしてこの式を使うのか、どうしてこの式が成り立つのか、常に考えるようにしましょう。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

