中学受験の算数で出題される単元「損益算」。売買算とも呼ばれ、品物の売買によって出る利益を求めます。普段から買い物をする大人からしてみれば馴染む深く簡単にイメージがつきますが、売買の経験があまりない子どもにとってはイメージがしづらく難しく感じることが多い単元です。
中学受験の算数では難しい損益算が出題されることもありますが、基本的なことが理解できていれば、簡単に解くことができます。
この記事では、損益算の解き方を紹介します。
- 算数が苦手な人
- 損益算を初めて学習する人
- 損益算が苦手な人
そのような人たちでも理解しやすいように、わかりやすく解説しています。この記事を読むことで、損益算とは何か理解でき、線分図を使った解き方を取得できます。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
損益算① 基本事項
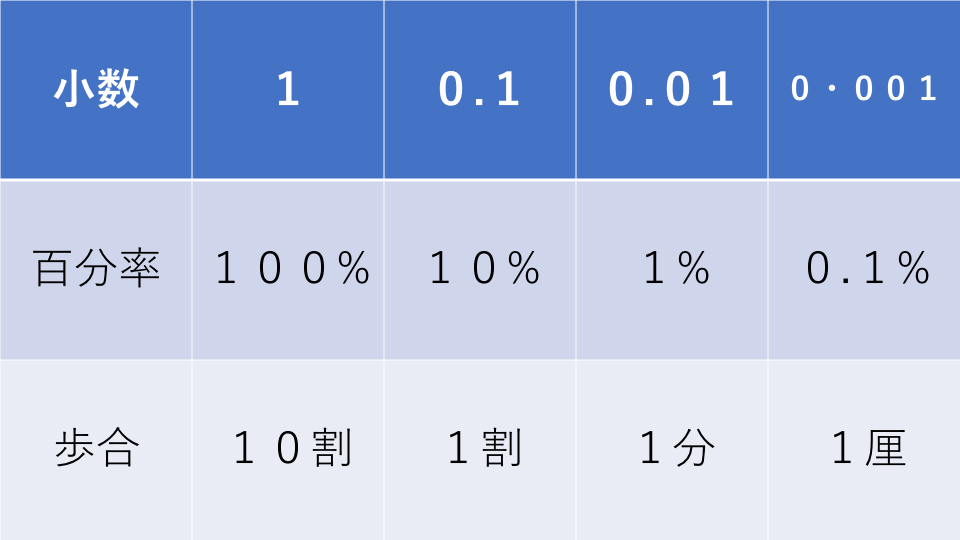
損益算を学習する前にいくつか理解しておかなければいけないことがあります。それは小数と百分率、歩合の関係です。
百分率とはもとにする量を100としたとき、それに対する1の割合を1%(パーセント)として表す表し方のことを言います。
割合がわからない人はこの記事(ここに内部リンク)を読んで理解してください。
百分率は小数で表した割合を100倍して求めます。
百分率=比べる量÷もとにする量×100
例えば0.5の割合があるとすると、百分率は、
0.5×100=50%になります。
百分率は今後出てくるので必ず理解してください。
歩合とは、もとにする量の0.1倍を1割、0.01倍を1分(ぶ)、0.001倍を厘(りん)と表す表し方を言います。
下の表は小数と百分率、歩合の関係を表したものです。必ず覚えてください。
次に覚えてもらいたいことは売買で使われる言葉です。中学受験の算数の損益算では、原価(仕入れ値)、定価、売値、利益この4つの言葉の意味と関係を理解しておくことがポイントです。
原価(仕入れ値)とは、販売するお店が、生産元か卸売り業者から買うときの値段のことを言います。
定価とは販売するお店の人が原価(仕入れ値)に利益を加えた値段のことを言います。
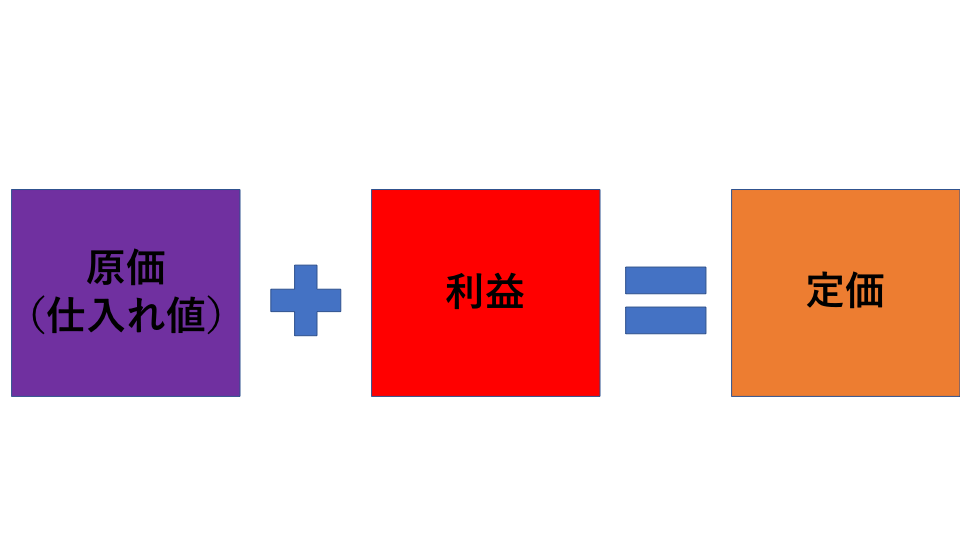
この値段が最初に値札として付けたものです。
定価で売れなかったとき、販売するお店の人が値段を下げて売ることがあります。このとき、定価から値引きして、実際にお客さんに売った値段のことを売値と言います。定価で売れたら定価が売値となります。
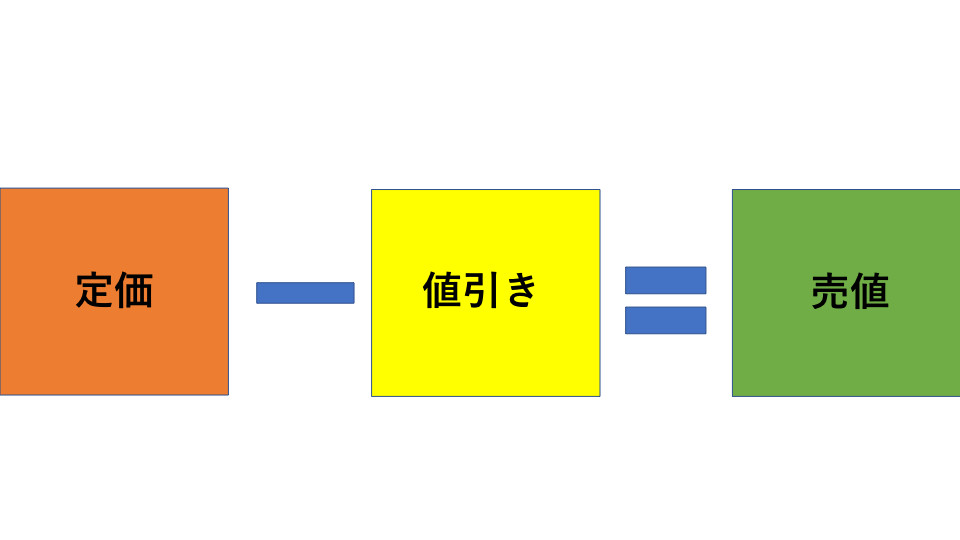
そして売値から仕入れ値を引いた金額が利益となります。
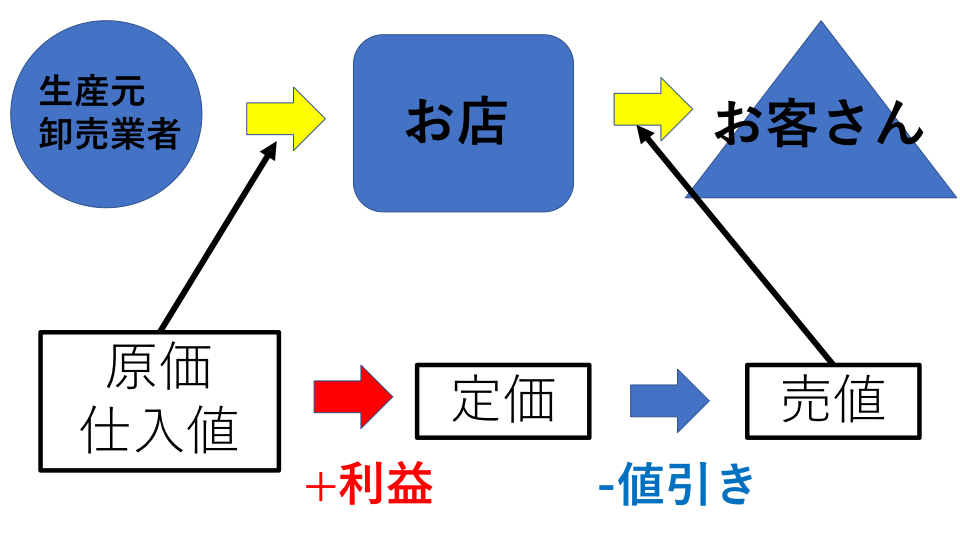
- 原価=お店が仕入れてきた値段
- 定価=お店が一番初めにつけた値段
- 売値=実際にお店がお客さんに売った値段
- 利益=売値−原価
損益算② 基本問題
例題1
ある商品に原価の2割の利益があるように定価をつけて4800円にしました。このときの原価を求めなさい。
解説
まずは線分図を書いて考えます。原価の2割の利益があるように定価をつけるので原価を1としたとき、定価は1.2になります。(2割は0.2のため)
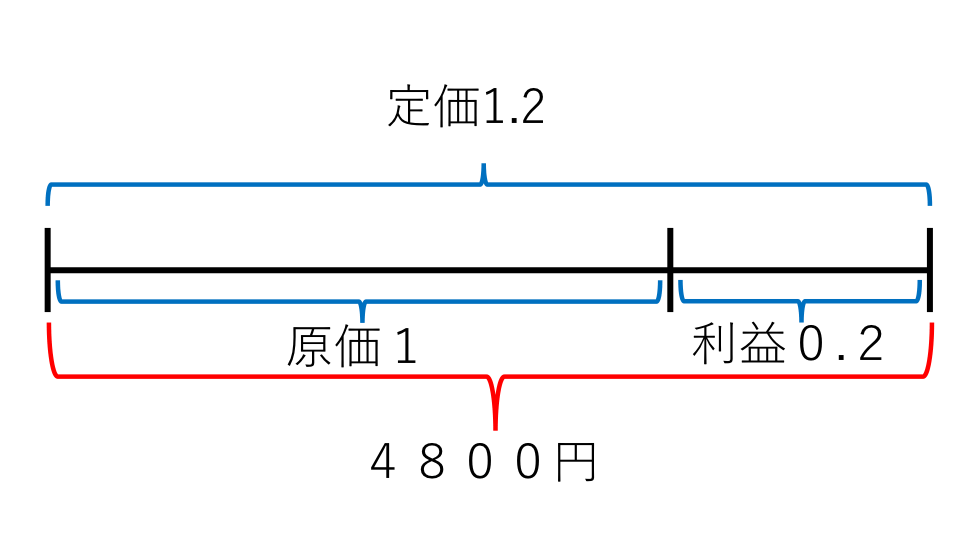
この線分図を見ると、4800円=原価×定価(1.2)ということがわかります。ここでは原価を求めたいので、式を変形すると、
原価=4800÷1.2=4000(円)
よって、答え 4000円
例題2
定価が7000円の商品を20%引きして、そこから100円引きしたところ、仕入れ値の10%の利益が上がりました。このときの商品の仕入れ値はいくらか求めなさい。
解説
例題1と同じようにして線分図を書いて考えます。この問題では定価しかわかっていないので、定価を基準にして考えていきます。すると以下のような線分図になります。
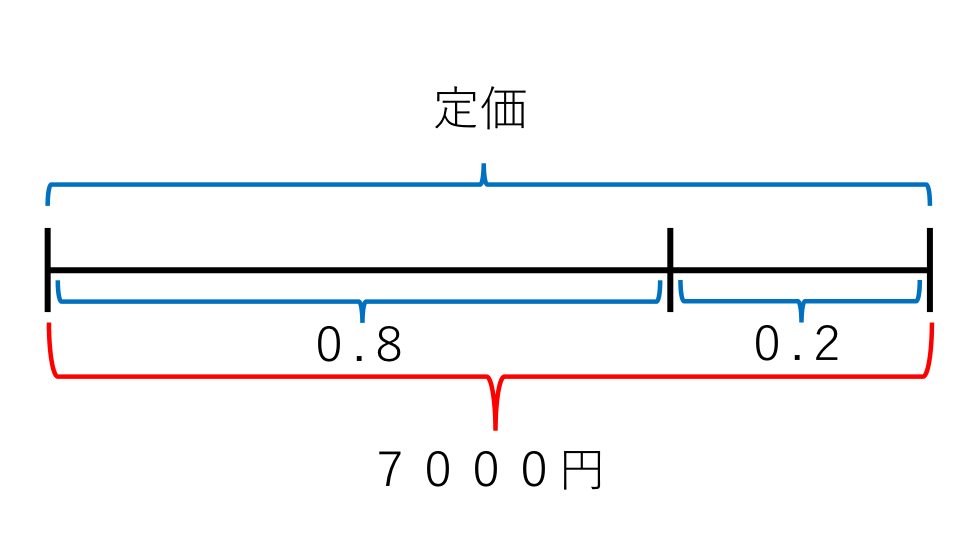
このとき定価の80%の部分が20%引きにした値段です。計算すると、
7000×0.8=5600(円)
この値段は100円引きする前の値段です。これを線分図に表すと以下のようになります。
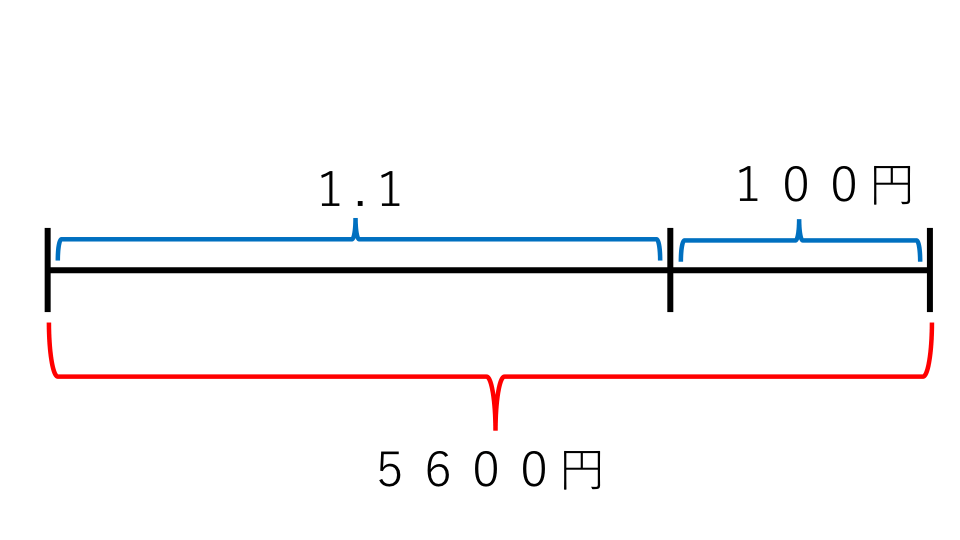
1.1の部分だけ求めるために、全体から100円を引くと、
5600−100=5500(円)
この値が仕入れ値を1と考えたときの1.1に対応します。(仕入れ値の10%の利益が上がるため)ですので、
1.1×仕入れ値=5500 となり、求めたいものは仕入れ値なので式を変形すると、
仕入れ値=5500÷1.1=5000(円)
よって、答え 仕入れ値5000円
損益算③ 応用問題
例題3
ある商品に、仕入れ値の3割の利益があるように定価をつけました。しかしあまり売れなかったので、定価の1割引きにして売ることにしました。そのときの売値が11700円でした。仕入れ値を求めなさい。
解説
線分図を書いて考えます。問題文からは売値しかわからないので、売値を基準にして考えます。売値を基準にして考えたときの線分図は以下のようになります。
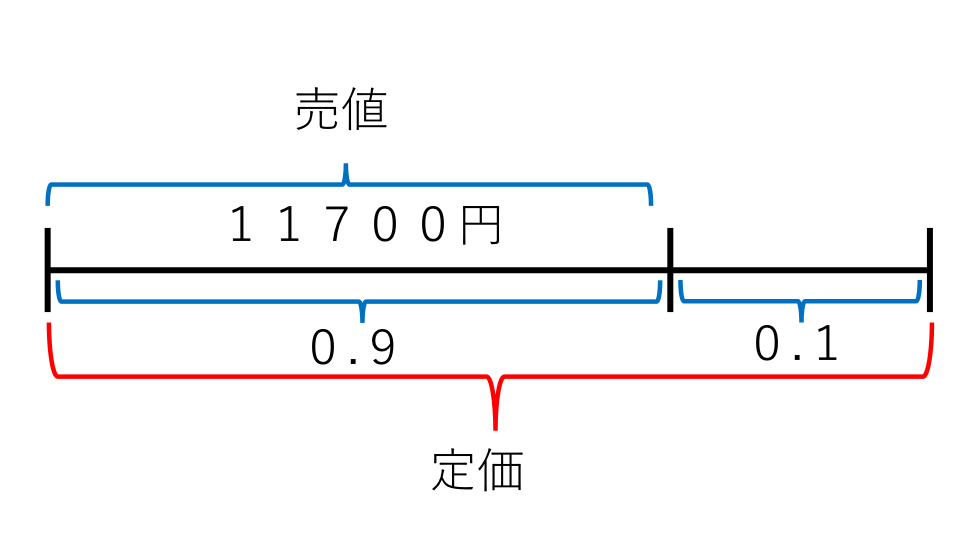
この線分図から売値は定価の0.9倍になっていることがわかります。ですので式は、
定価×0.9=11700(円) となり、式を変形すると、
定価=11700÷0.9=13000(円) となります。
定価がわかったので、定価を基準にして線分図を書くと以下のようになります。
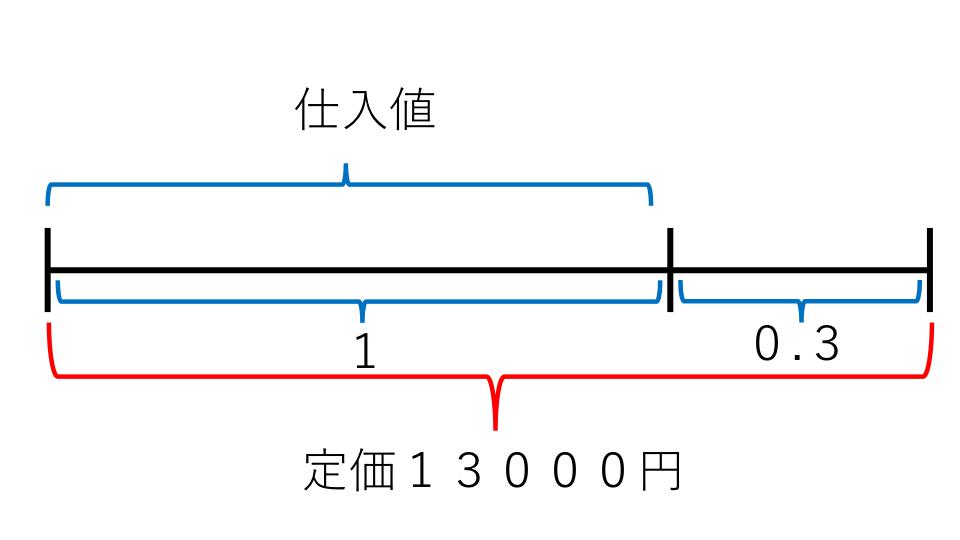
この線分図から定価は仕入れ値の1+0.3=1.3倍になっていることがわかります。ですので式は、
定価=仕入れ値×1.3 となるので、式を変形すると、
仕入れ値=13000÷1.3=10000(円)
よって、答え10000円
例題4
ある商品の売り上げの個数は7月、8月の2ヶ月続けて前の月の売り上げ個数の20%増しになりました。7月の売り上げ個数が480個のとき、8月の売り上げ個数は6月の売り上げ個数より何個多いか求めなさい。
解説
7月の売り上げ個数がわかっているので、7月の売り上げ個数を基準にして、6月の売り上げ個数を考えると線分図は以下のようになります。
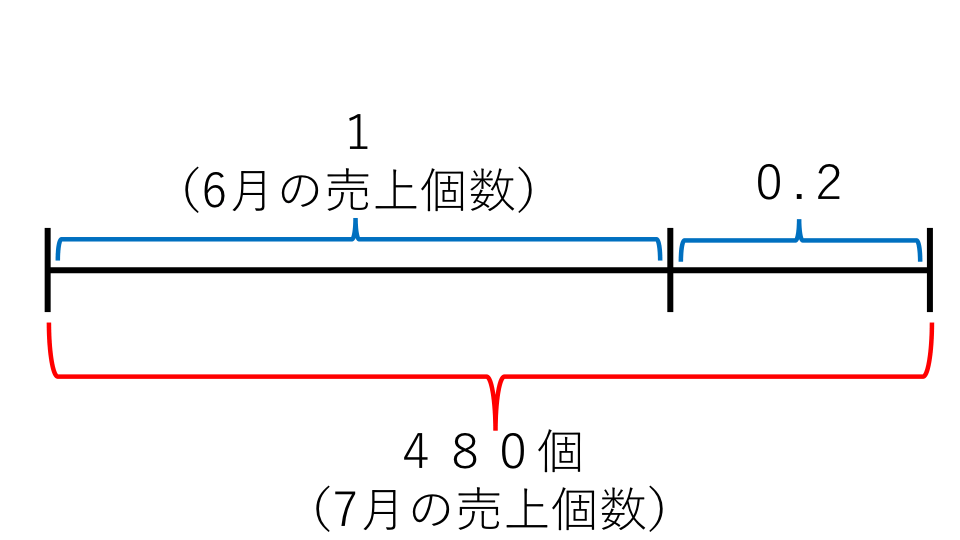
この線分図より、6月の売り上げ個数の1.2倍が7月の売り上げ個数とわかるので、式は、
7月の売り上げ個数=6月の売り上げ個数×1.2 となり式を変形すると、
6月の売り上げ個数=480÷1.2=400(個)
これで6月の売り上げ個数がわかりました。次に8月の売り上げ個数を求めていきます。7月の売り上げ個数を基準にして、8月の売り上げ個数を考えると線分図は以下のようになります。
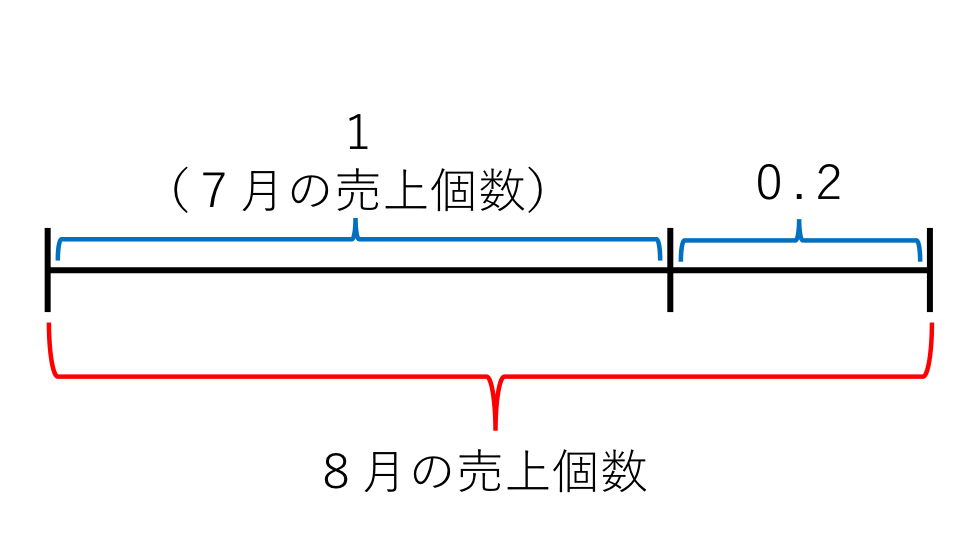
線分図より、8月の売り上げ個数は7月の売り上げ個数の1.2倍になることがわかるので、式は、
8月の売り上げ個数=480×1.2=576(個)
これで6月、8月の個数がわかったので差を求めると、
576-400=176(個)
よって、答え 176個
まとめ
いかがだったでしょうか?複雑な損益算でも、基準を考えて線分図を使って解くことで簡単に求めることができたと思います。
今回お伝えしたやり方と売買の用語の意味を十分に理解してより多くの問題を解き、損益算を完璧に理解してください。最後までご覧頂きありがとうございました。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

